Quadratic Equations Problems
Number of problems found: 583
- A rectangle 15
A rectangle is 5 cm longer its width. It areas is 6 cm square. What are the dimensions of the rectangle. - The length 20
The length and breadth of a rectangular park are in the ratio 8:5. A path,1.5 m wide, running all around the outside of the park has an area of 594 sq m. Find the dimensions of the park. - A field
A field is in the shape of a trapezium whose parallel sides are 25 m and 10 m and the non parallel sides are 14 m and 13 m. Find the area of the field. - The product 18
The product of two consecutive natural numbers which are multiples of 3 is equal to 810. Find the two numbers.
- Four numbers 3
What least number must be added to each of the numbers 6,15,20 and 43 to make them proportional? - The sum 51
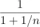The sum of two numbers is 100 and difference is 37 . Find the difference between their squares. - Reciprocal in equation
A positive number, when increased by 10 equals 200 times its reciprocal. What is the number? - A plane 3
A plane left 30 minutes later than the scheduled time and in order to reach the destination 1500 km away in time, it has to increase the speed by 250 km/hr from the usual speed. Find its usual speed. - Usual speed 2
A passenger train takes 1 h less for a journey of 120 km.If its speed increased by 10 k/h from its usual speed. What is its usual speed?
- By selling
By selling an article for $ 21, a trader loses as much percent as the cost price of the article. Find the cost price. - Palidrom
A number consists of two digits whose product is 24. When 18 is subtracted from the number, the digits change their places. Find the number. - Reciprocals - sum
The sum of the two numbers is 15. If the sum of their reciprocals is 5/18, find the numbers. - Square lawn
A square lawn has a 2 m wide path surrounding it. If the area of the path is 136 square meters, find the area of the lawn. - Usual speed
If the usual speed is reduced by 5 km per hour, a train takes 2 hours more to cover a distance of 300 km. Find the usual speed.
- Difference of squares 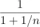If the difference between two numbers is 3 and the difference of their squares is 39, then find the larger number.
- By increasing
By increasing the speed of his car by 15 km/h, a person covers a 300 km distance in an hour less than before. What was the original speed? - The Product 16
The Product of two numbers is 96, and their quotient is 6. Find the numbers. - A boat 3
A boat takes 1 hour longer to go 36 km up a river than to return. If the river flows at 3 km/h, find the rate at which the boat travels in still water. - The difference 9 The difference of two numbers is 20 and their product is 56.25 times their difference. Find the LCM of the numbers.
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
