Rectangle practice problems - page 38 of 49
Number of problems found: 973
- Tank 28
The tank is shaped like a cuboid. The bottom is rectangular, one side of the rectangle is 40cm long, and the diagonal of this rectangle is 50cm. The height of the tank is 1.5m. We start filling the tank with water at a rate of 1 liter per second. No water - Diamond tile paving
How many diamond-shaped tiles with a side of 25 cm and a height of 20 cm are needed to pave a rectangular courtyard with sides of 30 m and 28 m if the joints represent 1/20 of the area? - Angle of diagonals
Calculate a rectangle's perimeter and area if its diagonal is 14 cm and the diagonals form an angle of 130°. - Irregular
Calculate the area and perimeter of the garden that was created from a rectangular plot measuring 10 by 20 meters after transferring one corner measuring 6 by 7 meters. The separated rectangular plot has parallel sides to the main plot. Did the perimeter - Gardens
The square garden is 3/4 of the area of the triangular garden, which has sides of 80 m, 50 m, and 50 m. How many meters of fence do we need to fence a square garden? - Described circle to rectangle
The rectangle with 6 cm and 4 cm sides was a circumscribed circle. What part of the circle area determined by the circumscribed circle occupies a rectangle? Express in perctentages(%). - Rectangle diagonal ratio
The aspect ratio of the rectangle and its diagonal is 9:12:15. Calculate the area of the rectangle if the length of the diagonal is 105 cm. - Three plane objects
How can we calculate the perimeter of a triangle, square, and rectangle? - Rectangle
There is a rectangle with a length of 12 cm and a diagonal 8 cm longer than the width. Calculate the area of a rectangle. - Snow wall
The boys want to build a defensive wall out of the snow for the ballpark. They want it to be 5 meters long and 1.5 meters high. They can make and transfer 50 cm cubes from snow. How many such cubes must he make to build his wall? - Rectangle measurements
In the ABCD rectangle, the AB side is 16 cm long, and the AC diagonal is 20 cm long. Calculate the perimeter and area of the rectangle. - Room wallpaper calculation
How many square meters of wallpaper will we need to cover the walls of a room with dimensions of 3 m and 4 m if the room height is 2.5 m? A door with dimensions of 90 cm and 2 m leads to the room. There is one window 1 m wide and 1.5 m high. - Circle rectangle fit
Find out if a circle with a volume of 38.5 cm² fits into a rectangle with dimensions of 110 mm and 65 mm. - The room
The room has a cuboid shape with dimensions: length of 50m and width of 60 dm, and height of 300 cm. Calculate how much this room will cost (a floor is not painted) if the window and door area is 15% of the total area and 1m² costs 15 euros. - Rectangle Side from Diagonal Calculate the other side of the rectangle if one side and the length of the diagonal are known: a = 3cm u = 5cm b =?
- Three shapes
1/5 of a circle is shaded. The area's ratio of a square and the sum of a| rectangle and the circle is 1:2. 60% of the square is shaded, and 1/3 of the rectangle is shaded. What is the ratio of the area of the circle to that of the rectangle? - The rectangle 5
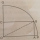The rectangle OABC has one vertex at O, the center of a circle, and a second vertex, A, 2 cm from the edge of the circle, as shown. The vertex A is also 7 cm from C. The points B and C lie on the circumference of the circle. a. What is the radius? b. Find - Side and diagonal
Find the circumference and the area of the rectangle if given: side a = 8 cm diagonal u = 10 cm. - Central park in city
The city park has the shape of a rectangle of 180 meters in length and 120 meters in width. People make their walk through the center of the park from one corner to the second. Calculate how many meters this way is shorter than walking along the path arou - Acreage
What acreage has a rectangular plot whose diagonal is 34 meters long, and one side has a length of 16 meters? ...
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
