Planimetrics - practice problems
The planimetrics studies plane measurements, including angles, distances, and areas. In other words, it involves the measurement and calculation of shapes in a two-dimensional plane. Typical problems include finding the perimeter and area of plane shapes.Planimetry is a subfield of geometry that focuses exclusively on plane figures (circles, triangles, quadrilaterals) and their:
- Mutual positions (perpendicularity, parallelism),
- Metric properties (circumference, area),
- Construction tasks (using compasses and ruler).
Example:
- Planimetry: Calculation of the area of a circle S = π r2 .
- Stereometry: Calculation of the volume of a sphere V = 43π r3 .
Planimetry is therefore a part of geometry that is limited to two-dimensional figures.
Number of problems found: 3688
- Piece of land
A farmer has a piece of land in the shape of a parallelogram. The two adjacent sides measure 15 meters and 10 meters. How much fencing is needed to enclose the entire garden? - The perimeter 13
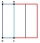The perimeter of a rectangle is 22cm. What are its dimensions if it has a maximum area? - Rectangle - S2
I need help calculating the area and perimeter of a rectangle with a length of 8 cm and a width of 5 cm. - Triangle - same sides
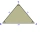Can the sides of a triangle have lengths of 11, 11, and 14? If so, what kind of triangle is it? - Parallelogram - simple One of the sides and the corresponding height of a parallelogram are 4 cm and 3 cm respectively. Find the area of the parallelogram.
- A gardener
A gardener wants to fence a circular garden of diameter 21 m. Find the length of the rope he needs to purchase, if he makes 2 rounds of fence. Also find the cost of the rope, if it costs $0.40 per meter. - Circular pizza
The radius of a circular pizza is 6 inches. What is the approximate circumference of the pizza? (Use π = 3.14) - Two wipers
What A car has two wipers which do not overlap. Each wiper has a blade of length 21 cm, sweeping through an angle of 120°. Find the total area cleaned at each sweep of the blades. - Polygon with x
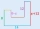All lines in the picture are perpendicular. Find the perimeter of the given polygon. - Rhombus tiles
The floor of a building consists of 3000 rhombus-shaped tiles, and each of its diagonals is 45 cm and 30 cm in length. Find the cost of polishing the floor at the rate of $4 per square meter. - A circular track
The inner circumference of a circular track is 220 m, and the width of the track is 7 m. Calculate the cost of putting up a fence along the outer circle at the rate of 50 USD/m. - Interior angles 4
How many degrees are in the sum of the interior angles of a quadrilateral? - Number of sides
Find the number of sides of a regular polygon whose each exterior angle has a measure of 45°. - Parallelogram - angles
In a parallelogram ABCD, if angle alpha measures ∠A = 70°, find all the other angles. - Front porch
Jon's front porch is 8 feet wide and 12 feet long. Jon wants to stain the wood on the porch next weekend. The stain costs $1.00 per square foot. How much will it cost to buy enough stain for the whole porch? - Circle's diameter
The diameter of a circle is 32 inches. What is the circle's area? Use π(pi) ≈ 3.14 and round your answer to the nearest hundredth. - A room
A room is 8 2/3 m by 5 1/4 m. What is the area of the room? - A model
A model of a house is built on a base that measures 7 3/4 inches wide and 9 1/5 inches long. What is the area of the model house based? - Yd2 to ft2 unit conversion
If a room requires 25.4 square yards of carpeting, what is the area of the floor in units of ft2? (3 ft. = 1 yd.) - A triangular
A triangular frame has sides that measure 15’-7",20’-4", and 26’-2". What is the total length of the three sides?
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
