Circle practice problems
A circle is a geometric shape that consists of all points that are a fixed distance, called the radius, away from a central point called the center. The distance around the circle is called the circumference and the region enclosed by the circle is called the area of the circle. The formula for the circumference of a circle is C = 2πr, where C is the circumference, r is the radius, and π is a mathematical constant, the Ludolph number, approximately equal to 3.1415926.The formula for the area of a circle is A = πr2, where A is the area and r is the radius.
Number of problems found: 992
- Blue region
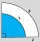 Find the area of the blue region on the picture.
Find the area of the blue region on the picture. - Circle's diameter
 The diameter of a circle is 32 inches. What is the circle's area? Use π(pi) ≈ 3.14 and round your answer to the nearest hundredth.
The diameter of a circle is 32 inches. What is the circle's area? Use π(pi) ≈ 3.14 and round your answer to the nearest hundredth. - Concentric circles 4
 One circle has a radius of 98 cm, and a second concentric circle has a 1m 26 cm radius. How much longer is the circumference of the second circle than that of the first?
One circle has a radius of 98 cm, and a second concentric circle has a 1m 26 cm radius. How much longer is the circumference of the second circle than that of the first? - The radius 2
 The radius of a circle is increased by 5%. What is the percentage increase in their circumference area?
The radius of a circle is increased by 5%. What is the percentage increase in their circumference area? - Planetary system
 Robert has built a mechanical model solar system with three balls representing planets at the end of rods. Each rod is attached to the center, representing the Sun. The planets are lined up when he turns on the motor. The innermost planet makes a revoluti
Robert has built a mechanical model solar system with three balls representing planets at the end of rods. Each rod is attached to the center, representing the Sun. The planets are lined up when he turns on the motor. The innermost planet makes a revoluti - Find all 2
 Find all the complex solutions (write the answer in the form x+iy) of the system. {|z-12|/|z-8i|=5/3 ; |z-4|=|z-8|
Find all the complex solutions (write the answer in the form x+iy) of the system. {|z-12|/|z-8i|=5/3 ; |z-4|=|z-8| - A rope for cow
 Find the length of a rope by which a cow must be tethered in order that it may be able to graze an area of 154 sq m .
Find the length of a rope by which a cow must be tethered in order that it may be able to graze an area of 154 sq m . - Pizza diameter
 If an 18-inch pizza costs $16.99 and is cut into 12 slices, what is the cost per square inch?
If an 18-inch pizza costs $16.99 and is cut into 12 slices, what is the cost per square inch? - Circle inscribed square
 What is the area of the circle that can be inscribed in a square of 10 cm?
What is the area of the circle that can be inscribed in a square of 10 cm? - Two circles 3
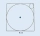 Two circles are inscribed in a square whose side is 4 cm. Find the radius of the smaller circle.
Two circles are inscribed in a square whose side is 4 cm. Find the radius of the smaller circle. - Incircle to circumcircle
 Find the ratio of the areas of the incircle and the circumcircle of a square.
Find the ratio of the areas of the incircle and the circumcircle of a square. - Hands of a clock
 At what time between 11 and 12 O'clock will the hands of a clock be at an angle of 180°?
At what time between 11 and 12 O'clock will the hands of a clock be at an angle of 180°? - Merly
 Merly prepared the table for lunch. She put a place mat that measures 5 dm long and 3 dm wide; she placed a plate on it with a diameter of 3 dm. How many mats can be seen on the table?
Merly prepared the table for lunch. She put a place mat that measures 5 dm long and 3 dm wide; she placed a plate on it with a diameter of 3 dm. How many mats can be seen on the table? - At 5:16
 At 5:16, what is the acute angle between a minute hand and an hour hand?
At 5:16, what is the acute angle between a minute hand and an hour hand? - Largest circle
 If the largest possible circle is cut off from a 8 cm × 4 cm rectangle, what is the area in sq cm of the remaining portion?
If the largest possible circle is cut off from a 8 cm × 4 cm rectangle, what is the area in sq cm of the remaining portion? - ET inscribed circle
 An equilateral triangle has been inscribed in a circle with a radius of 4 cm . Find the area of the shaded region.
An equilateral triangle has been inscribed in a circle with a radius of 4 cm . Find the area of the shaded region. - A gardener
 A gardener wants to fence a circular garden of diameter 21 m. Find the length of the rope he needs to purchase, if he makes 2 rounds of fence. Also find the cost of the rope, if it costs $0.40 per meter.
A gardener wants to fence a circular garden of diameter 21 m. Find the length of the rope he needs to purchase, if he makes 2 rounds of fence. Also find the cost of the rope, if it costs $0.40 per meter. - Garden hose
 Miguel wound a garden hose around a circular real. If the diameter of the real is 10 inches, how many inches of hose was wound on the first full turn of the real round? The answer to the nearest whole inch, use 3.14 for pi.
Miguel wound a garden hose around a circular real. If the diameter of the real is 10 inches, how many inches of hose was wound on the first full turn of the real round? The answer to the nearest whole inch, use 3.14 for pi. - A circular track
 The inner circumference of a circular track is 220 m, and the width of the track is 7 m. Calculate the cost of putting up a fence along the outer circle at the rate of 50 USD/m.
The inner circumference of a circular track is 220 m, and the width of the track is 7 m. Calculate the cost of putting up a fence along the outer circle at the rate of 50 USD/m. - A cone 3
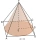 A cone has a diameter of x cm and a slant height of y cm. A square pyramid has a base side length of x cm and a slant height of y cm. Which has the greater surface area? Explain.
A cone has a diameter of x cm and a slant height of y cm. A square pyramid has a base side length of x cm and a slant height of y cm. Which has the greater surface area? Explain.
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
