The right triangle altitude theorem - practice problems
Euclid was a Greek mathematician and philosopher. He left us with two important but simple theorems that apply in a right triangle.Euclid's first theorem (about height): The area of the square constructed above the height of the right triangle (h) is equal to the area of the rectangle constructed from both sections of the hypotenuse (c1 and c2):
h2=c1c2
Or: The height in a right triangle is the geometric mean of two sections of the hypotenuse.
h=c1⋅c2
Euclid's second theorem - about the hypotenuse: The area of the square constructed above the hypotenuse of a right-angled triangle is equal to the area of the rectangle constructed from the hypotenuse and the segment of the hypotenuse adjacent to this hypotenuse.
a2=c⋅c1
b2=c⋅c2
Or: The hypotenuse of a right triangle is the geometric diameter of the hypotenuse and the adjacent section of the hypotenuse.
a=c⋅c1
It is usually teach in high school. The Pythagorean theorem can be easily proved using Euclid's theorems.
Direction: Solve each problem carefully and show your solution in each item.
Number of problems found: 71
- An isosceles triangle
 An altitude is drawn from the vertex of an isosceles triangle, forming a right angle and two congruent triangles. As a result, the altitude cuts the base into two equal segments. The length of the altitude is 18 inches, and the length of the base is 15 in
An altitude is drawn from the vertex of an isosceles triangle, forming a right angle and two congruent triangles. As a result, the altitude cuts the base into two equal segments. The length of the altitude is 18 inches, and the length of the base is 15 in - PQR - Euclid
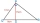 Find the length of line segment PR - leg of the right triangle PQR. PQ=17 cm PS=15 cm QS=8 cm; Point S is the height touch point with a hypotenuse of the RQ.
Find the length of line segment PR - leg of the right triangle PQR. PQ=17 cm PS=15 cm QS=8 cm; Point S is the height touch point with a hypotenuse of the RQ. - Euclid2
 The ABC right triangle with a right angle at C is side a=29 and height v=17. Calculate the perimeter of the triangle.
The ABC right triangle with a right angle at C is side a=29 and height v=17. Calculate the perimeter of the triangle. - Leg and height
 Solve right triangle with height v = 7.8 m and shorter cathetus b = 15 m.
Solve right triangle with height v = 7.8 m and shorter cathetus b = 15 m. - Height of right RT
 The right triangle ABC has a hypotenuse c 9 cm long and a part of the hypotenuse cb = 3 cm. How long is the height of this right triangle?
The right triangle ABC has a hypotenuse c 9 cm long and a part of the hypotenuse cb = 3 cm. How long is the height of this right triangle? - Isosceles IV
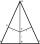 In an isosceles triangle ABC is |AC| = |BC| = 13 and |AB| = 10. Calculate the radius of the inscribed (r) and described (R) circle.
In an isosceles triangle ABC is |AC| = |BC| = 13 and |AB| = 10. Calculate the radius of the inscribed (r) and described (R) circle. - Triangle ABC
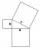 Right triangle ABC with right angle at the C, |BC|=19, |AB|=26. Calculate the height of the triangle hAB to the side AB.
Right triangle ABC with right angle at the C, |BC|=19, |AB|=26. Calculate the height of the triangle hAB to the side AB. - Euklid4
 The legs of a right triangle have dimensions 241 m and 34 m. Calculate the length of the hypotenuse and the height of this right triangle.
The legs of a right triangle have dimensions 241 m and 34 m. Calculate the length of the hypotenuse and the height of this right triangle. - Proof PT
 Can you easily prove Pythagoras' theorem using Euclidean theorems? If so, do it.
Can you easily prove Pythagoras' theorem using Euclidean theorems? If so, do it. - Area of RT
 The right triangle has orthogonal projections of legs to the hypotenuse lengths 15 cm and 9 cm. Determine the area of this triangle.
The right triangle has orthogonal projections of legs to the hypotenuse lengths 15 cm and 9 cm. Determine the area of this triangle. - Circle in rhombus
 An inscribed circle is in the rhombus. Contact points of touch divide the sides into parts of length 14 mm and 9 mm. Calculate the circle's area.
An inscribed circle is in the rhombus. Contact points of touch divide the sides into parts of length 14 mm and 9 mm. Calculate the circle's area. - RT triangle and height
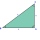 Calculate the remaining sides of the right triangle if we know side b = 4 cm long and height to side c h = 2.4 cm.
Calculate the remaining sides of the right triangle if we know side b = 4 cm long and height to side c h = 2.4 cm. - Spruce height
 How tall was the spruce that was cut at an altitude of 8m above the ground, and the top landed at a distance of 15m from the heel of the tree?
How tall was the spruce that was cut at an altitude of 8m above the ground, and the top landed at a distance of 15m from the heel of the tree? - Euclid1
 The right triangle ABC has hypotenuse c = 20 cm. How large sections cut height hc=9 cm on the hypotenuse c?
The right triangle ABC has hypotenuse c = 20 cm. How large sections cut height hc=9 cm on the hypotenuse c? - Area of RT
 Calculate the right triangle area in which the hypotenuse has length 14 and one hypotenuse segment has length 5.
Calculate the right triangle area in which the hypotenuse has length 14 and one hypotenuse segment has length 5. - Right-angled - legs
 The lengths of legs are a = 7.2 cm and b = 10.4 cm in the right-angled triangle ABC. Calculate: a) lengths of the sections of the hypotenuse b) height to the hypotenuse c
The lengths of legs are a = 7.2 cm and b = 10.4 cm in the right-angled triangle ABC. Calculate: a) lengths of the sections of the hypotenuse b) height to the hypotenuse c - Euclid 5
 Calculate the length of remain sides of a right triangle ABC if a = 7 cm and height vc = 5 cm.
Calculate the length of remain sides of a right triangle ABC if a = 7 cm and height vc = 5 cm. - Hypotenuse and height
 In a right triangle is length of the hypotenuse c = 195 cm and height hc = 70 cm. Determine the length of both triangle legs.
In a right triangle is length of the hypotenuse c = 195 cm and height hc = 70 cm. Determine the length of both triangle legs. - Sides of the triangle
 Calculate triangle sides where its area is S = 84 cm² and a = x, b = x + 1, xc = x + 2
Calculate triangle sides where its area is S = 84 cm² and a = x, b = x + 1, xc = x + 2 - Euclid3
 Calculate the height and sides of the right triangle if one leg is a = 100 km and the section of hypotenuse adjacent to the second leg cb = 14 km.
Calculate the height and sides of the right triangle if one leg is a = 100 km and the section of hypotenuse adjacent to the second leg cb = 14 km.
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
