An isosceles triangle
An altitude is drawn from the vertex of an isosceles triangle, forming a right angle and two congruent triangles. As a result, the altitude cuts the base into two equal segments. The length of the altitude is 18 inches, and the length of the base is 15 inches. Find the triangle's perimeter. Round to the nearest tenth of an inch.
Final Answer:
Tips for related online calculators
See also our right triangle calculator.
Calculation of an isosceles triangle.
See also our trigonometric triangle calculator.
Calculation of an isosceles triangle.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
arithmeticplanimetricsGrade of the word problem
Related math problems and questions:
- Right isosceles triangle
 The right isosceles triangle has an altitude x drawn from the right angle to the hypotenuse, dividing it into two equal segments. One segment is 5 cm long. What is the area of the triangle?
The right isosceles triangle has an altitude x drawn from the right angle to the hypotenuse, dividing it into two equal segments. One segment is 5 cm long. What is the area of the triangle? - Right 24
 The right isosceles triangle has an altitude x drawn from the right angle to the hypotenuse, dividing it into two unequal segments. One segment is 5 cm long. What is the area of the triangle? Thank you.
The right isosceles triangle has an altitude x drawn from the right angle to the hypotenuse, dividing it into two unequal segments. One segment is 5 cm long. What is the area of the triangle? Thank you. - Nonagon
 Calculate the area and perimeter of a regular nonagon if its radius of the inscribed circle is r = 10cm.
Calculate the area and perimeter of a regular nonagon if its radius of the inscribed circle is r = 10cm. - Isosceles
 A flower bed has the shape of an isosceles triangle with a base of 25m and sides of 30m. Calculate the maximum number of flowers that can be planted in this bed, assuming that one flower requires about 8 dm² of square area. Round the result to the nearest
A flower bed has the shape of an isosceles triangle with a base of 25m and sides of 30m. Calculate the maximum number of flowers that can be planted in this bed, assuming that one flower requires about 8 dm² of square area. Round the result to the nearest - Isosceles triangle perimeter
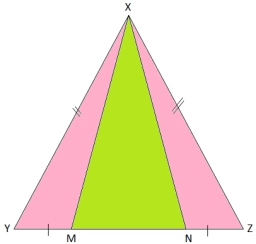
 Two isosceles triangles have the same angle at the vertex opposite the base. The first one has a base of 12 cm and a leg of 9 cm. The other has a 16 cm long base. Calculate the perimeter of the second triangle.
Two isosceles triangles have the same angle at the vertex opposite the base. The first one has a base of 12 cm and a leg of 9 cm. The other has a 16 cm long base. Calculate the perimeter of the second triangle. - Piece of a wire
 A piece of wire is bent into the shape of a triangle. Two sides have lengths of 24 inches and 21 inches. The angle between these two sides is 55°. What is the length of the third side to the nearest hundredth of an inch? A: The length of the third side is
A piece of wire is bent into the shape of a triangle. Two sides have lengths of 24 inches and 21 inches. The angle between these two sides is 55°. What is the length of the third side to the nearest hundredth of an inch? A: The length of the third side is - Garden hose
 Miguel wound a garden hose around a circular real. If the diameter of the real is 10 inches, how many inches of hose was wound on the first full turn of the real round? The answer to the nearest whole inch, use 3.14 for pi.
Miguel wound a garden hose around a circular real. If the diameter of the real is 10 inches, how many inches of hose was wound on the first full turn of the real round? The answer to the nearest whole inch, use 3.14 for pi.
