Right isosceles triangle
The right isosceles triangle has an altitude x drawn from the right angle to the hypotenuse, dividing it into two equal segments. One segment is 5 cm long. What is the area of the triangle?
Correct answer:
Tips for related online calculators
Looking for calculator of harmonic mean?
Looking for a statistical calculator?
See also our right triangle calculator.
Calculation of an isosceles triangle.
See also our trigonometric triangle calculator.
Looking for a statistical calculator?
See also our right triangle calculator.
Calculation of an isosceles triangle.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
statisticsarithmeticplanimetricsUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- Right 24
The right isosceles triangle has an altitude x drawn from the right angle to the hypotenuse, dividing it into two unequal segments. One segment is 5 cm long. What is the area of the triangle? Thank you. - An isosceles triangle
An altitude is drawn from the vertex of an isosceles triangle, forming a right angle and two congruent triangles. As a result, the altitude cuts the base into two equal segments. The length of the altitude is 18 inches, and the length of the base is 15 in - Segments on the hypotenuse
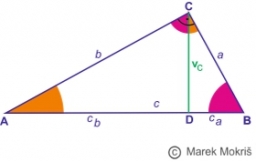
A right triangle ABC has a hypotenuse of c=26cm. How many segments does the height vc=12 cm cut out on the hypotenuse c? What are the lengths of the sides a and b? What are the angles at the vertices A and B? - Touch circle
Point A has a distance (A, k) = 10 cm from a circle k with radius r = 4 cm and center S. Calculate: a) the distance of point A from the point of contact T if the tangent to the circle is drawn from point A b) the distance of the contact point T from the l - Chord 24
A chord with length t = r times the square root of two divides a circle with radius r into two circular segments. What is the ratio of the areas of these segments? - Height of right RT
The right triangle ABC has a hypotenuse c 9 cm long and a part of the hypotenuse cb = 3 cm. How long is the height of this right triangle? - Triangle KLM
In the rectangular triangle KLM, where |KL|=m is the hypotenuse (sketch it!). Find the length of the leg k and the height of triangle h if the hypotenuse's segments are known MK = 5cm and ml = 15 cm.
