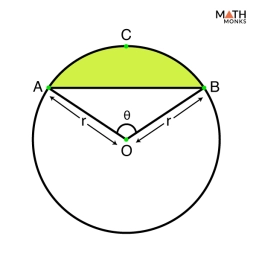
Chord 24
A chord with length t = r times the square root of two divides a circle with radius r into two circular segments. What is the ratio of the areas of these segments?
Final Answer:
Tips for related online calculators
Check out our ratio calculator.
See also our right triangle calculator.
Do you want to convert time units like minutes to seconds?
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
See also our right triangle calculator.
Do you want to convert time units like minutes to seconds?
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
You need to know the following knowledge to solve this word math problem:
arithmeticplanimetricsbasic operations and conceptsgoniometry and trigonometryUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- Colored area
 How large is the area colored brown inside a square of side 6 cm if each of the four brown circular segments is from a circle with a radius of the length of the square's side? The length of the circular segments is equal to the length of the side of the s
How large is the area colored brown inside a square of side 6 cm if each of the four brown circular segments is from a circle with a radius of the length of the square's side? The length of the circular segments is equal to the length of the side of the s - Three segments
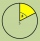 The circle is divided into three segments. Segment A occupies 1/4 of the area. Segment B occupies 1/3 of the area. What part is occupied by section C? In what proportion are areas A: B: C?
The circle is divided into three segments. Segment A occupies 1/4 of the area. Segment B occupies 1/3 of the area. What part is occupied by section C? In what proportion are areas A: B: C? - Circular pool
 The pool's base is a circle with a radius r = 10 m, excluding a circular segment that determines the chord length of 10 meters. The pool depth is h = 2m. How many hectoliters of water can fit into the pool?
The pool's base is a circle with a radius r = 10 m, excluding a circular segment that determines the chord length of 10 meters. The pool depth is h = 2m. How many hectoliters of water can fit into the pool? - Chord - TS v2
 The radius of circle k measures 72 cm. Chord GH = 11 cm. What is TS?
The radius of circle k measures 72 cm. Chord GH = 11 cm. What is TS? - Concentric circles
 A circle K with radius r = 8 cm is given. How big a radius must a smaller concentric circle divides a circle K into two parts with the same area?
A circle K with radius r = 8 cm is given. How big a radius must a smaller concentric circle divides a circle K into two parts with the same area? - Concentric circles and chord
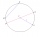 In a circle with a diameter d = 10 cm, a chord with a length of 6 cm is constructed. What radius has the concentric circle while touching this chord?
In a circle with a diameter d = 10 cm, a chord with a length of 6 cm is constructed. What radius has the concentric circle while touching this chord? - Chord
 In a circle with a radius r=60 cm is the chord, 4× longer than its distance from the center. What is the length of the chord?
In a circle with a radius r=60 cm is the chord, 4× longer than its distance from the center. What is the length of the chord?
