Arcsine - practice problems
The arcsine is the inverse of the trigonometric sine function. The argument of the function is a number (ratio of the length of the opposite side to the hypotenuse), and the output is the angle in radians.Task: Work through each problem with care and demonstrate your solution process for each one.
Number of problems found: 62
- Angle of inclination
Find the angle of inclination of a ramp that rise for 80 cm and is 200 cm long. - Triangle 90
Triangle made by 6 cm 4.5 cm and 7.5 cm. what angles does it make? - Parallelogram 44
Parallelogram ABCD has an area of 32 cm2, lABl=8cm, lBCl=5cm. Calculate the sizes of its interior angles. - In a regular 5
In a regular triangular prism ABCV, the deviation of the side wall and the base plane is α = 45°. Determine the deviation of the side edge and the base plane. - Graduation of the track
The gradient of the track is 9 per mile, and the distance per kilometer (on the slope) [AC] = is 560m. Determine the angle alpha and the distance [AB] = the height between A and B. A / | B/____________C - Segments on the hypotenuse
A right triangle ABC has a hypotenuse of c=26cm. How many segments does the height vc=12 cm cut out on the hypotenuse c? What are the lengths of the sides a and b? What are the angles at the vertices A and B? - Chord 24
A chord with length t = r times the square root of two divides a circle with radius r into two circular segments. What is the ratio of the areas of these segments? - Perimeter of a circle segment
A circle with a diameter of 30 cm is cut by a chord t = 16 cm. Calculate the perimeter and area of the smaller segment. - Central angle A circle k with a center at point S and a radius of 6 cm is given. Calculate the size of the central angle subtended by a chord 10 cm long.
- Kite deltoid angles
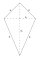A paper kite is shaped like a deltoid ABCD, with two shorter sides 30 cm long, two longer sides 51 cm long, and a shorter diagonal 48 cm long. Determine the sizes of the internal angles of the given deltoid. - In plane 2
A triangle ABC is located in the plane with a right angle at vertex C, for which the following holds: A(1, 2), B(5, 2), C(x, x+1), where x > -1. a) determine the value of x b) determine the coordinates of point M, which is the midpoint of line segment - Archaeologists
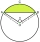Archaeologists need to find out the size of the vessel if the sherd found was in the shape of a circular section with a length of 12 cm and a height of 3 cm. What is the area of this section? - Quadrilateral triangle segment
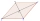The quadrilateral ABCD is symmetrical about the diagonal AC. The length of AC is 12 cm, the length of BC is 6 cm, and the interior angle at vertex B is right. points E and F are given on the sides AB, and AD so that the triangle ECF is equilateral. Determ - Felix
Calculate how much land Felix Baumgartner saw after jumping from 36 km above the ground. The radius of the Earth is R = 6378 km. - Acceleration - down a slope
A skier goes down a slope 66 m long in a uniformly accelerated motion in 10 seconds. With what acceleration was it moving, and what is the slope of the slope? - The cosine law
Solve the unknown dimensions for the following triangle: Triangle ABC: Angle A=43 degrees, b=7.0cm, c=6.0cm Question 1. Angle B with units written as degrees Question 2. Angle C with units written as degrees Question 3. a, rounded to the nearest tenth of - A rhombus 4
A rhombus has a side length of 10 cm. Find the angles at each corner of the rhombus if the shorter of the two diagonals measures 7 cm. Give your answers to the nearest degree and give clear geometric reasoning at each stage of your solution. - Colored area
How large is the area colored brown inside a square of side 6 cm if each of the four brown circular segments is from a circle with a radius of the length of the square's side? The length of the circular segments is equal to the length of the side of the s - Cosine
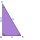Cosine and sine theorem: Calculate all unknown values (sides and angles) of the triangle ABC. a = 20 cm; b = 15 cm; γ = 90°; c =? cm; α =? °; β =? ° - Rectangle ABCD
The rectangle ABCD is given whose | AB | = 5 cm, | AC | = 8 cm, ∢ | CAB | = 30°. How long is the other side, and what is its area?
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
