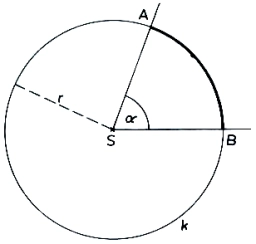
Central angle
A circle k with a center at point S and a radius of 6 cm is given. Calculate the size of the central angle subtended by a chord 10 cm long.
Final Answer:
Showing 1 comment:
Dr. Math
1. Use the chord length formula:
The length L of a chord subtending a central angle θ (in radians) in a circle of radius r is:
Plugging in L = 10 cm and r = 6 cm:
2. Solve for θ :
In degrees:
The length L of a chord subtending a central angle θ (in radians) in a circle of radius r is:
L = 2r sin(θ2)
Plugging in L = 10 cm and r = 6 cm:
10 = 2 × 6 × sin(θ2) ⇒ sin(θ2) = 1012 = 56.
2. Solve for θ :
θ2 = arcsin(56) ⇒ θ = 2 arcsin(56).
In degrees:
θ ≈ 2 × 56.44° ≈ 112.89°.
Tips for related online calculators
Do you want to convert time units like minutes to seconds?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
You need to know the following knowledge to solve this word math problem:
geometryalgebraplanimetricsgoniometry and trigonometryUnits of physical quantitiesGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- A chord
In a circle radius of 6 cm, a chord is drawn 3 cm from the center. Calculate the angle subtended by the chord at the center of the circle. Hence find the length of the minor arc cut off by the chord. - Magnitude 25411
There is a circle with a radius of 10 cm and its chord, which is 12 cm long. Calculate the magnitude of the central angle that belongs to this chord. - Two chords
There is a given circle k (center S, radius r). From point A, which lies on circle k, are starting two chords of length r. What angle do chords make? Draw and measure. - Circular segment
Calculate the area of a circular segment if the radius r = 80 cm and the central angle is α = 110°. - Calculate 3561 There is a 12 cm long chord in a circle with a radius of 10 cm. Calculate the distance of the chord from the center of the circle.
- The chord - angle
The distance of the chord from the center is 6 cm. The central angle is 60°. Calculate the area of the circular segment. - Intersection + tangents
Given a circle with a radius r = 4 cm and a point A for which |AS| applies = 10 cm. Calculate the distance of point A from the intersection of the points of contact of the tangents drawn from point A to the circle.
