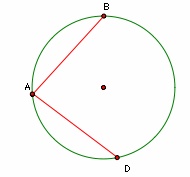
Two chords
There is a given circle k (center S, radius r). From point A, which lies on circle k, are starting two chords of length r. What angle do chords make? Draw and measure.
Correct answer:
Tips for related online calculators
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
Units of physical quantities:
Themes, topics:
Grade of the word problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Equilateral 14873
There is a circle with a radius of 2.5 cm and point A, which lies on it. Write an equilateral triangle ABC in the circle. - Two circles
Two circles with the same radius, r = 1, are given. The center of the second circle lies on the circumference of the first. What is the area of a square inscribed in the intersection of given circles? - Two chords
From the point on the circle with a diameter of 8 cm, two identical chords are led, which form an angle of 60°. Calculate the length of these chords. - Convex angle
There is a circle k (S; r), and a point A, which lies on this circle. There is also a point B on the circumference, for which it is true that in one direction, it is five times further from point A than in the opposite direction (around the circumference
- Mrak - cloud
It is given segment AB, which is 12 cm in length, on which one side of the square MRAK is laid. MRAK's side length is 2 cm shown. MRAK gradually flips along the line segment AB, and point R leaves a paper trail. Draw the whole track of point R until the s - Circle
The circle touches two parallel lines, p, and q, and its center lies on line a, which is the secant of lines p and q. Write the equation of the circle and determine the coordinates of the center and radius. p: x-10 = 0 q: -x-19 = 0 a: 9x-4y+5 = 0 - Chord
The point on the circle is the endpoint of diameter and endpoint of the chord length of the radius. What angle between chord and diameter?
