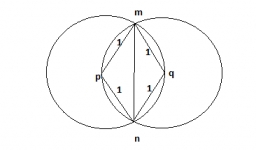
Two circles
Two circles with the same radius, r = 1, are given. The center of the second circle lies on the circumference of the first. What is the area of a square inscribed in the intersection of given circles?
Correct answer:
Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
Related math problems and questions:
- Two chords
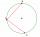There is a given circle k (center S, radius r). From point A, which lies on circle k, are starting two chords of length r. What angle do chords make? Draw and measure. - Two parallel chords
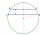In a circle 70 cm in diameter, two parallel chords are drawn so that the circle's center lies between the chords. Calculate the distance of these chords if one of them is 42 cm long and the second 56 cm. - Goat and circles
What is the radius of a circle centered on the other circle, and is the intersection of the two circles equal to half the area of the first circle? This task is the mathematical expression of the role of agriculture. The farmer has circular land on which - Two annuluses
The area of the annular circle formed by two circles with a common center is 100 cm². The radius of the outer circle is equal to twice the radius of the inner circle. Determine the outside circle radius in centimeters. - Concentric circles
There is given a Circle K with a radius r = 8 cm. How large must a radius have a smaller concentric circle that divides the circle K into two parts with the same area? - Annular area The square with side a = 1 is inscribed and circumscribed by circles. Find the annular area.
- Quadrilateral 78874
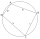Given is a quadrilateral ABCD inscribed in a circle, with the diagonal AC being the circle's diameter. The distance between point B and the diameter is 15 cm, and between point D and the diameter is 18 cm. Calculate the radius of the circle and the perime - Circle and square
An ABCD square with a side length of 100 mm is given. Calculate the circle's radius that passes through vertices B, C, and the center of the side AD. - The rectangle 5
The rectangle OABC has one vertex at O, the center of a circle, and a second vertex A is 2 cm from the edge of the circle, as shown. The vertex A is also a distance of 7 cm from C. The point B and C lie on the circumference of the circle. a. What is the r - Ratio of sides
Calculate the area of a circle with the same circumference as the circumference of the rectangle inscribed with a circle with a radius of r 9 cm so that its sides are in a ratio of 2 to 7. - Square ABCD
Construct a square ABCD with center S [3,2] and the side a = 4 cm. Point A lies on the x-axis. Construct a square image in the displacement given by oriented segment SS'; S` [-1 - 4]. - Four circles
1) Calculate the circle radius if its area is 400 cm square 2) Calculate the radius of the circle whose circumference is 400 cm. 3) Calculate circle circumference if its area is 400 cm square 4) Calculate the circle's area if the perimeter is 400 cm. - Ratio of squares
A circle is given in which a square is inscribed. The smaller square is inscribed in a circular arc formed by the square's side and the circle's arc. What is the ratio of the areas of the large and small squares? - Find the 13
Find the equation of the circle inscribed in the rhombus ABCD where A[1, -2], B[8, -3], and C[9, 4]. - Chord 2
Point A has a distance of 13 cm from the circle's center with a radius r = 5 cm. Calculate the length of the chord connecting the points T1 and T2 of contact of tangents led from point A to the circle. - Circumference 3589
Calculate the circle's radius if the circumference and area are in a 2: 5 ratio. - Circle
The circle touches two parallel lines, p, and q, and its center lies on line a, which is the secant of lines p and q. Write the equation of the circle and determine the coordinates of the center and radius. p: x-10 = 0 q: -x-19 = 0 a: 9x-4y+5 = 0
