Quadrilateral circle radius
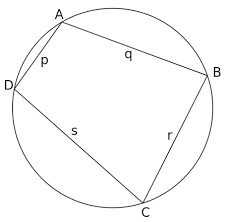
Given is a quadrilateral ABCD inscribed in a circle, with the diagonal AC being the circle's diameter. The distance between point B and the diameter is 15 cm, and between point D and the diameter is 18 cm. Calculate the radius of the circle and the perimeter of the quadrilateral ABCD.
Your answer:
Your answer:
Tips for related online calculators
Are you looking for help with calculating roots of a quadratic equation?
Do you have a linear equation or system of equations and are looking for a solution? Or do you have a quadratic equation?
See also our right triangle calculator.
Do you have a linear equation or system of equations and are looking for a solution? Or do you have a quadratic equation?
See also our right triangle calculator.
You need to know the following knowledge to solve this word math problem:
algebraarithmeticplanimetryGrade of the word problem
Related math problems and questions:
- Construct rhombus
Construct rhombus ABCD if given diagonal length | AC | = 8 cm, inscribed circle radius r = 1.5 cm - Square circles
Calculate the length of the described and inscribed circle to the square ABCD with a side of 5 cm. - Two circles
Two circles with the same radius, r = 1, are given. The center of the second circle lies on the perimeter of the first. What is the area of a square inscribed in the intersection of given circles? - Two circles 3
Two circles are inscribed in a square with a side of 4 cm. Find the radius of the smaller circle. - Circle radius calculation
Point B is the center of the circle. The line AC touches the circles at point C and applies AB = 20 cm and AC = 16 cm. What is the radius of the circle BC? - Triangle
In triangle ABC, point S is the incentre (centre of the inscribed circle). The area of quadrilateral ABCS equals four-fifths of the area of triangle ABC. The side lengths of triangle ABC are all integers expressed in centimetres, and the perimeter of tria - Circle radius calculation
The area of the two circles is in a 4:9 ratio. The larger circle has a diameter of 18 cm. Calculate the radius of the smaller circle.
