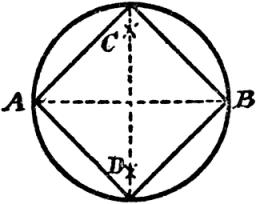
Square circles
Calculate the length of the described and inscribed circle to the square ABCD with a side of 5cm.
Correct answer:
Tips for related online calculators
See also our right triangle calculator.
Do you want to convert length units?
See also our trigonometric triangle calculator.
Do you want to convert length units?
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- Square inscribed
Find the length of the side of the square ABCD, which is inscribed to a circle k with a radius of 10 cm. - Calculate 5499
Calculate the area of the circle, which is described by a square with a side length of 7.5 cm. - Circumference 4278
An inscribed circle is also described as an equilateral triangle with a side length of 8 cm. How many cm is the circumference of the inscribed circle smaller than the circumference of the described circle? - Quatrefoil
Calculate the quatrefoil area, inscribed in a square with a side of 6 cm.
- Circular ring
A square with an area of 16 centimeters is inscribed circle k1 and described to circle k2. Calculate the area of the circular ring, which circles k1, and k2 form. - Calculate 8252
Calculate in cm² the area of a circle whose diameter is equal to the length of the diagonal of a square ABCD with a side of 4cm. - Rhombus and inscribed circle
It is given a rhombus with side a = 6 cm and the inscribed circle r = 2 cm radius. Calculate the length of its two diagonals.
