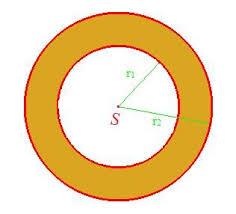
Circular ring
A square with an area of 16 centimeters is inscribed circle k1 and described to circle k2. Calculate the area of the circular ring, which circles k1, and k2 form.
Your answer:
Your answer:
Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
arithmeticplanimetryGrade of the word problem
Related math problems and questions:
- Circular lawn
Around a circular lawn area is a 2 m wide sidewalk. The outer edge of the sidewalk is a curb whose width is 2 m. The Curbstone and the inner side of the sidewalk together form concentric circles. Calculate the area of the circular lawn, and the result rou - Circle arc + section
Calculate the length of the arc of a circle and the volume of a circular section if the circle's radius is 8.3 centimeters and the central angle alpha=104 degrees. - Circles 2
Calculate the area of the region between the circumscribed circle and the inscribed circle of a triangle with sides 29 cm, 16 cm, and 21 cm. - Circle arc
A circular sector has an arc length of 7.16 m and an area of 146.69 m². Calculate the radius of the circle and the size of the central angle. - Annulus
Two concentric circles with radii 1 and 9 surround the annular circle. This ring is inscribed with n circles that do not overlap. Determine the highest possible value of n. - Ratio of squares
A circle is given, and a square is inscribed. The smaller square is inscribed in a circular arc formed by the square's side and the circle's arc. What is the ratio of the areas of the large and small squares? - Annular area
The square with side a = 1 is inscribed and circumscribed by circles. Find the annular area.
