Diagonal - practice problems
A diagonal is a line segment connecting two non-adjacent vertices of a polygon or two non-adjacent corners of a polyhedron. In a polygon with n sides, there are n(n-3)/2 diagonals total. For rectangles, diagonals are equal and bisect each other; their length is found using the Pythagorean theorem: d = √(l² + w²). In squares, diagonals are equal, perpendicular, and form 45° angles with sides, with length d = s√2. Diagonals of rhombi are perpendicular bisectors of each other.Number of problems found: 546
- Diagonals
What is the number of diagonals of a decagon? - Incircle to circumcircle
Find the ratio of the areas of the incircle and the circumcircle of a square. - Two circles 3
Two circles are inscribed in a square whose side is 4 cm. Find the radius of the smaller circle. - Circle inscribed square
What is the area of the circle that can be inscribed in a square of 10 cm? - The area 5
The area of a rhombus is 144 sq cm. If one of the diagonals is double the other, find the length of the diagonals. - Smaller square
Let the points A, B, C and D are midpoints of the sides of the square PQRS. If the area of PQRS is 100 sq cm, what is the area of the smaller square ABCD? - Rhombus = area, diagonal
The area of a rhombus is 144 sq cm. One of its diagonals is twice the other. How long is the shorter diagonal? - Rhombus 36 Rhombus ABCD with side 8 cm long has diagonal BD 11.3 cm long. Find angle DAB.
- RT with rectangle
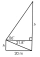In the diagram, find the lengths h and b. One rectangle and one right triangle share one side. We know two angles and the length of the common side, as shown in the picture. - Parallelogram - right angles
In parallelogram ABCD; AB = 16 cm, BC = 12 cm and diagonal AC = 20 cm. Find the area of the parallelogram. - The rhombus (a,d) Find the area of a rhombus, one side of which measures 20 cm, and one diagonal 24 cm.
- ABCD rhombus ABCD is a rhombus with sides 10.5cm. If the length of the diagonal AC=15.8cm, using cosine formula. a. calculate the length of the diagonal BD correct to the nearest cm b. the angles of the rhombus to the nearest degree.
- Grassland and goat
An unfenced grassland is a right triangle ABC with AB = 4m, BC = 8m, and AC as hypotenuse. A goat is tied to a 5-m long rope with its stake at point O, which is 2m from side AB and 2m from the prolongation of side BC through corner B. Then: 1. How far is - Three inscribed objects
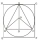A circle is inscribed in a square. An equilateral triangle of side 4√3 is inscribed in that circle. Find the length of the diagonal of the square. - Four points There are 4 nonlinear points. How many triangles can form by joining them?
- Cuboid - sum of edges length
Calculate the cuboid's dimensions if the sum of its edges is 19 cm. The body's diagonal size is 13 cm, and its volume is 144 cm³. The total surface area is 192 cm². - Diagonal
Can a rhombus have the same length, diagonal, and side? - Diagonal
Can it be a diagonal diamond twice longer than its side? - Hexagon diagonal count
Does a hexagon have 275 diagonals? - Square
Calculate the side of a square with a diagonal measurement of 10 cm.
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
