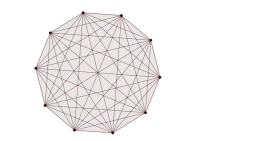
Diagonals
What x-gon has 54 diagonals?
Final Answer:
Tips for related online calculators
Are you looking for help with calculating roots of a quadratic equation?
Would you like to compute the count of combinations?
Do you have a linear equation or system of equations and are looking for a solution? Or do you have a quadratic equation?
Would you like to compute the count of combinations?
Do you have a linear equation or system of equations and are looking for a solution? Or do you have a quadratic equation?
You need to know the following knowledge to solve this word math problem:
combinatoricsalgebraplanimetryUnits of physical quantitiesGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- N-gon
How many diagonals does a convex 30-gon have? - Parallelogram perimeter area
The parallelogram has side a = 58 cm and diagonals u = 89 cm and v = 52 cm. Calculate the perimeter and area of this parallelogram. - 6-gon
The perimeter of a regular hexagon is 154. Calculate its circumradius (radius of a circumscribed circle). - Rhombus - diagonals
Rhombus ABCD has diagonals u₁ and u₂ that make an angle of 60° with each other. Side a = 80 cm and side b = 50 cm. Calculate the area of the rhombus. - Regular n-gon
Which regular polygon has a circumscribed circle radius of r = 10 cm and an inscribed circle radius of p = 9.962 cm? - 6 regular polygon
A regular six-sided polygon has a side 5 cm long. Calculate its area. Compare how many more cm² (square centimeters) has a circle inscribed the 6-gon. - Polygon 42
Which polygon has 42 more diagonals than sides?
