Geometry - practice problems
Geometry is a branch of mathematics that studies the properties and relationships of points, lines, figures, and solids.It deals with two-dimensional (e.g., triangle, circle) and three-dimensional objects (e.g., cube, sphere), their perimeters, areas, volumes, and relative positions.
It is used in architecture, engineering, art, and the natural sciences to describe and analyze shapes and structures.
The basic parts of geometry are planimetry (geometry in the plane) and stereometry (geometry in space).
Number of problems found: 3238
- Two vertically
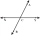 Two vertically opposite angles are (x-20)° and 85°; then, find the value of x.
Two vertically opposite angles are (x-20)° and 85°; then, find the value of x. - Vertical axis
 Find the perpendicular distance of the point A=(5,-7) from the y-axis.
Find the perpendicular distance of the point A=(5,-7) from the y-axis. - Points
 The point A has coordinates (3, 3). The point A moves 5 units to the left and 4 units down to a new point B. (a) Write down the coordinates of point B. (b) Which quadrant is point B in?
The point A has coordinates (3, 3). The point A moves 5 units to the left and 4 units down to a new point B. (a) Write down the coordinates of point B. (b) Which quadrant is point B in? - Sarah 4
 Sarah and Jamal were learning partners in math class and were working independently. They each started at the point (−2, 5) and moved 3 units vertically in the plane. Each student arrived at a different endpoint. How is this possible? Explain and list the
Sarah and Jamal were learning partners in math class and were working independently. They each started at the point (−2, 5) and moved 3 units vertically in the plane. Each student arrived at a different endpoint. How is this possible? Explain and list the - At noon 3
 At noon, the temperature was 45˚ F. For the next ten hours, the temperature fell at a steady rate. The graph represents the temperature every hour since noon. At 5:00 temperature was 20°F. At what rate did the temperature fall?
At noon, the temperature was 45˚ F. For the next ten hours, the temperature fell at a steady rate. The graph represents the temperature every hour since noon. At 5:00 temperature was 20°F. At what rate did the temperature fall? - There 35
 There are three points on a straight line: A, BC. If CD = 8x, DE = 3, and CE = x + 10, what is CD? Simplify your answer and write it as a proper fraction, mixed number, or integer.
There are three points on a straight line: A, BC. If CD = 8x, DE = 3, and CE = x + 10, what is CD? Simplify your answer and write it as a proper fraction, mixed number, or integer. - Collinear lines
 Points A, B, and C are collinear, and B lies between A and C. If AC = 48, AB = 2x + 2, and BC = 3x + 6, what is BC?
Points A, B, and C are collinear, and B lies between A and C. If AC = 48, AB = 2x + 2, and BC = 3x + 6, what is BC? - The slope 2
 What is the slope of the line that passes through the points (-4, -7) and (-2,-19)? Write your answer in the simplest form.
What is the slope of the line that passes through the points (-4, -7) and (-2,-19)? Write your answer in the simplest form. - Line in normal form
 Try to find the equation of a line given two points in the form Ax+By=C. passes through the points: (2,1) and (-2,2)
Try to find the equation of a line given two points in the form Ax+By=C. passes through the points: (2,1) and (-2,2) - Complement and supplement
 Find the measure of an angle if 7 times its complement is 10° less than 3 times its supplement.
Find the measure of an angle if 7 times its complement is 10° less than 3 times its supplement. - Equation of a line
 Find the equation of a line that passes through (1, 3) and is parallel to the line y = - 2x + 4.
Find the equation of a line that passes through (1, 3) and is parallel to the line y = - 2x + 4. - A linear
 A linear function has a y-intercept of -12 and a slope of 3/2. What is the equation of the line?
A linear function has a y-intercept of -12 and a slope of 3/2. What is the equation of the line? - X intercept
 Given: 3y+2x=-6 Calculate the X-intercept.
Given: 3y+2x=-6 Calculate the X-intercept. - Y-intercept
 Find the y-intercept of the graph (-3,-3), (4,3), (8,3). The x-intercept is 1/2.
Find the y-intercept of the graph (-3,-3), (4,3), (8,3). The x-intercept is 1/2. - Equation of the line
 Find the equation of the line through (1, 2) with slope 3.
Find the equation of the line through (1, 2) with slope 3. - Line segments
 There are three line segments on the line: the length of MN = 3 1/2, the length of NO= 2 3/4, and the length of OP=1 2/3. Find the length of line segment MP. Write your answer as a mixed number.
There are three line segments on the line: the length of MN = 3 1/2, the length of NO= 2 3/4, and the length of OP=1 2/3. Find the length of line segment MP. Write your answer as a mixed number. - The temperature 41
 The temperature drops by 5 degrees per Hour in Alaska. It is 4 degrees at 6 PM. What will the temperature be at 9 PM?
The temperature drops by 5 degrees per Hour in Alaska. It is 4 degrees at 6 PM. What will the temperature be at 9 PM? - Matrices 2
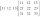 Suppose A=(1 6 3 −2) B=(4 −3 −4 3) find 2A+3B
Suppose A=(1 6 3 −2) B=(4 −3 −4 3) find 2A+3B - Consecutive Interior Angles
 PQRS is a trapezium in which PQ is parallel to SR and ∠P = 130 ̊, ∠Q = 110 ̊. Find the remaining angles.
PQRS is a trapezium in which PQ is parallel to SR and ∠P = 130 ̊, ∠Q = 110 ̊. Find the remaining angles. - Angle over circle
 In the figure, O is the center of the circle and AB is tangent at B. If angle OAB is 28 degrees find angle AOB. Figure is not scaled.
In the figure, O is the center of the circle and AB is tangent at B. If angle OAB is 28 degrees find angle AOB. Figure is not scaled.
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
