Thales' theorem - practice problems
The Tales theorem says that if A, B, C are points on a circle, where AC is the diameter of the circle, then the angle ABC is the right angle. The Tales circle is the set of vertexes of right angles of right triangles constructed above the diameter of the circle. The Tales theorem results directly from the inscribed angle theorem. Simple proof - the radius joining point C divides a rectangular triangle into two isosceles triangles, and the sum of the angles in each triangle is 180°.Instructions: Solve each problem carefully and provide a detailed solution for every item.
Number of problems found: 46
- Angle over circle
In the figure, O is the center of the circle and AB is tangent at B. If angle OAB is 28 degrees find angle AOB. Figure is not scaled. - Construction - Euclid
Using Euclid's theorems, construct a triangle ABC with height on side c and size v = √8 cm. Choose the length of the hypotenuse c correctly. Write the construction procedure. - Rectangle construction diagonal
Construct a rectangle ABCD if a = 8cm and the length of the diagonal AC is 13cm. Measure the length of the sides of the rectangle. - Largest possible area
A right-angled triangle was inscribed in a circle with a diameter of 20 cm, whose hypotenuse is the circle's diameter and has the largest possible area. Calculate the area of this triangle. - Triangle - BAC angle
The given line is a BC length of 6 cm. Construct a triangle so that the BAC angle is 50° and the height to the side is 5.5 cm. Thank you very much. - Triangle construction sides
Sestroj triangle HOP, if o = 6 cm, h = 8 cm and | PHO | = 90 ° - Quadrilateral ABCD
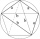Construct a quadrilateral ABCD if AB = 10cm, AD = 6cm, DC = 6.5cm and angle BCD = 90 degrees. - Triangle construction sides
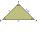Construct a right triangle ABC with the hypotenuse AB: a) | AB | = 72 mm, | BC | = 51 mm b) | AB | = 58 mm, | AC | = 42 mm - Lunes of Hippocrates
Calculate the sum of the area of the so-called Hippocratic lunas, which were cut above the legs of a right triangle (a = 6cm, b = 8cm). Instructions: First, calculate the area of the semicircles above all sides of the ABC triangle. Compare the sum of the - Draw triangle
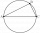Construct right triangle MNO with hypotenuse o = 5 cm and angle MNO = 37° - Touch circle
Point A has a distance (A, k) = 10 cm from a circle k with radius r = 4 cm and center S. Calculate: a) the distance of point A from the point of contact T if the tangent to the circle is drawn from point A b) the distance of the contact point T from the l - MIT 1869
You know the length of parts 9 and 16 of the hypotenuse, at which a right triangle's hypotenuse is divided by a height. The task is to find the lengths of the sides of the triangle and the length of line x. This assignment was part of the Massachusetts In - Construct
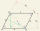Construct a rhombus ABCD with side a = 7cm, b = 5cm, whose diagonal e is perpendicular to side b. - Square equal rhombus
Construct a square that has the same area as a rhombus ABCD if |AB| = 5cm, |AD| = 4cm, and angle |DAB| = 30°. - Triangle side drawing
Draw a right triangle with side a = 5 cm, c = 8 cm. The right angle is at vertex C. What is the size of side b? - The amphitheater
The amphitheater has the shape of a semicircle, the spectators sit on the perimeter of the semicircle, and the stage forms the diameter of the semicircle. Which spectators, P, Q, R, S, and T, see the stage at the greatest viewing angle? - Triangle circle calculation
The following elements are known in the right triangle ABC: a = 10 cm, height to side c h = 9.23 cm. Calculate o, R (radius of the inscribed circle), r (radius of the inscribed circle). - Construct rhombus
Construct rhombus ABCD if given diagonal length | AC | = 8cm, inscribed circle radius r = 1.5cm - Parallels and one secant
There are two different parallel lines, a, b, and line c, that intersect the two parallel lines. Draw a circle that touches all lines at the same time. - Construct rhombus - MO
Construct the diamond ABCD so that its diagonal BD is 8 cm and the distance of apex B from the line AD is 5 cm. Specify all possibilities. How long is a side of a rhombus?
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
