Largest possible area
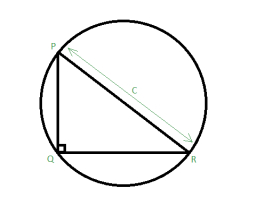
A right-angled triangle was inscribed in a circle with a diameter of 20 cm, whose hypotenuse is the circle's diameter and has the largest possible area. Calculate the area of this triangle.
Final Answer:
Tips for related online calculators
See also our right triangle calculator.
You need to know the following knowledge to solve this word math problem:
geometryplanimetricsbasic operations and conceptsGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Quadrilateral 78874
Given is a quadrilateral ABCD inscribed in a circle, with the diagonal AC being the circle's diameter. The distance between point B and the diameter is 15 cm, and between point D and the diameter is 18 cm. Calculate the radius of the circle and the perime - RT = legs, circle
One leg of a right triangle ABC has length a= 14 cm and the radius of the circle inscribed in this triangle r= 5 cm. Calculate the length of the hypotenuse and its other leg. - Concentric circles
In the circle with diameter, 13 cm is constructed chord 1 cm long. Calculate the radius of a concentric circle that touches this chord. - Prism
A right-angled prism, whose base is a right triangle with leg a = 3 cm and hypotenuse c = 6 cm, has the same volume as a cube with an edge length of 1 dm. a) Find the height of the prism b) Calculate the surface of the prism c) What percentage of the cube - Square circles
Calculate the length of the described and inscribed circle to the square ABCD with a side of 5cm. - Circles 2
Calculate the area bounded by the circumscribed and inscribed circle in a triangle with sides 29 cm, 16 cm, and 21 cm. - Concentric circles and chord
In a circle with a diameter d = 10 cm, a chord with a length of 6 cm is constructed. What radius has the concentric circle while touching this chord?
