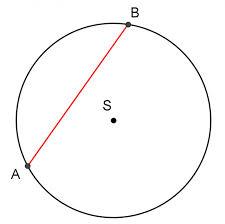
Concentric circles
In the circle with diameter, 13 cm is constructed chord 1 cm long. Calculate the radius of a concentric circle that touches this chord.
Correct answer:
Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
Related math problems and questions:
- Concentric circles and chord
In a circle with a diameter d = 10 cm, a chord with a length of 6 cm is constructed. What radius has the concentric circle while touching this chord? - Circles
In the circle with a radius, 7.5 cm is constructed of two parallel chords whose lengths are 9 cm and 12 cm. Calculate the distance of these chords (if there are two possible solutions, write both). - Magnitude 25411
There is a circle with a radius of 10 cm and its chord, which is 12 cm long. Calculate the magnitude of the central angle that belongs to this chord. - Two chords
In a circle with a radius of 8.5 cm, two parallel chords are constructed, the lengths of which are 9 cm and 12 cm. Find the distance of the chords in a circle. - Calculate 3561
There is a 12 cm long chord in a circle with a radius of 10 cm. Calculate the distance of the chord from the center of the circle. - Calculate 80636
Calculate the distance of a chord 19 cm long from the center of a circle with a diameter of 28 cm. - Common chord
The common chord of the two circles, c1 and c2, is 3.8 cm long. This chord forms an angle of 47° with the radius r1 in the circle c1. An angle of 24° 30' with the radius r2 is formed in the circle c2. Calculate both radii and the distance between the two - Circular flowerbed
We split the circular flowerbed with diameter 8 m by concentric circle to circle and annulus with the same area. Find the radius of the circle. - Circle annulus
There are two concentric circles in the figure. The chord of the larger circle, 10 cm long, is tangent to the smaller circle. What does annulus have? - Two parallel chords
In a circle 70 cm in diameter, two parallel chords are drawn so that the circle's center lies between the chords. Calculate the distance of these chords if one of them is 42 cm long and the second 56 cm. - MO circles
Juro built the ABCD square with a 12 cm side. In this square, he scattered a quarter circle with a center at point B passing through point A and a semicircle l with a center at the center of the BC side and passed point B. He would still build a circle th - Annulus
Two concentric circles form an annulus of a width of 10 cm. The radius of the smaller circle is 20 cm. Calculate the area of the annulus. - Concentric circles
There is given a Circle K with a radius r = 8 cm. How large must a radius have a smaller concentric circle that divides the circle K into two parts with the same area? - String 63794
The chord AB is in the circle k with a radius of 13 cm. The center C of the string AB is 5 cm from the center S of the circle. How long is the AB string? - Calculate 79144
The circle's radius is r=8.9 cm, and the chord AB of this circle has a length of 16 cm. Calculate the distance of chord AB from the center of the circle. - Chord
The point on the circle is the endpoint of diameter and endpoint of the chord length of the radius. What angle between chord and diameter? - Pavement
Calculate the length of the pavement that runs through a circular square with a diameter of 40 m if the distance of the pavement from the center is 15 m.
