Pythagorean theorem - practice problems
The Pythagorean Theorem states that in a right-angled triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides. This can be written as:c2 = a2 + b2
where c is the length of the hypotenuse, and a and b are the lengths of the other two sides.
Number of problems found: 1397
- Missing side length
Use the Pythagorean Theorem (a² + b²=c²) to find a unknown side length: a = 5; c = 13 ; b=? - Incircle to circumcircle
Find the ratio of the areas of the incircle and the circumcircle of a square. - Find area 2
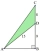Find the area of the green region in the given picture. Dimensions are shown. - The hypotenuse
The hypotenuse of a right-angled triangle is 20 meters. If the difference between the lengths of the other sides is 4 meters, find the other sides.
- A ladder 2
A ladder 10 m long reaches the window of a house 8 m above the ground. Find the distance of the foot of the ladder from the base of the wall. - Two circles 3
Two circles are inscribed in a square whose side is 4 cm. Find the radius of the smaller circle. - Isosceles triangle 17
One of the equal sides of an isosceles triangle is 13 cm and its perimeter is 50 cm. Find the area of the triangle. - Circle inscribed square
What is the area of the circle that can be inscribed in a square of 10 cm? - A chord 2
A chord of length 16 cm is drawn in a circle of radius 10 cm. Calculate the distance of the chord from the center of the circle.
- ET inscribed circle
An equilateral triangle has been inscribed in a circle with a radius of 4 cm . Find the area of the shaded region. - A field
A field is in the shape of a trapezium whose parallel sides are 25 m and 10 m and the non parallel sides are 14 m and 13 m. Find the area of the field. - Smaller square
Let the points A, B, C and D are midpoints of the sides of the square PQRS. If the area of PQRS is 100 sq cm, what is the area of the smaller square ABCD? - A right 3
A right triangle has a perimeter of 300 cm . its hypotenuse is 130cm. What are the lengths of the other sides . - Cosine - legs
Using the law of cosines, find the measurement of leg b if the givens are β=20°, a=10, and c=15.
- Rhombus 36
Rhombus ABCD with side 8 cm long has diagonal BD 11.3 cm long. Find angle DAB. - A tree 2
A tree is broken at a height of 6 m from the ground and its top touches the ground at a distance of 8 m from the base of the tree. Find the original height of the tree. - FGH right triangle Given a right triangle with leg lengths f and g, and hypotenuse h, if f = 7 cm and h = 11.2 cm, what is g?
- A triangle 7
A triangle lot has the dimensions a=15m, b=10m, and c=20m. What is the measure of the angle between the sides of b and c? - Two chords 6
A chord PQ is 10.4cm long, and its distance from the center of a circle is 3.7cm. Calculate the length of a second chord RS, which is 4.1cm from the center of this circle.
Mrs. Clarke is teaching a 5th-grade class. She is standing 40 feet in front of Valeria. Sarah is sitting to Valeria's right. If Sarah and Mrs. Clarke are 50 feet apart, how far apart are Valeria and Sarah?Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
