Area + Pythagorean theorem - practice problems
Number of problems found: 669
- The rhombus (a,d)
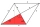 Find the area of a rhombus, one side of which measures 20 cm, and one diagonal 24 cm.
Find the area of a rhombus, one side of which measures 20 cm, and one diagonal 24 cm. - A field
 A field is in the shape of a trapezium whose parallel sides are 25 m and 10 m and the non parallel sides are 14 m and 13 m. Find the area of the field.
A field is in the shape of a trapezium whose parallel sides are 25 m and 10 m and the non parallel sides are 14 m and 13 m. Find the area of the field. - Isosceles triangle 17
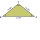 One of the equal sides of an isosceles triangle is 13 cm and its perimeter is 50 cm. Find the area of the triangle.
One of the equal sides of an isosceles triangle is 13 cm and its perimeter is 50 cm. Find the area of the triangle. - Grassland and goat
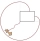 An unfenced grassland is a right triangle ABC with AB = 4m, BC = 8m, and AC as hypotenuse. A goat is tied to a 5-m long rope with its stake at point O, which is 2m from side AB and 2m from the prolongation of side BC through corner B. Then: 1. How far is
An unfenced grassland is a right triangle ABC with AB = 4m, BC = 8m, and AC as hypotenuse. A goat is tied to a 5-m long rope with its stake at point O, which is 2m from side AB and 2m from the prolongation of side BC through corner B. Then: 1. How far is - Incircle to circumcircle
 Find the ratio of the areas of the incircle and the circumcircle of a square.
Find the ratio of the areas of the incircle and the circumcircle of a square. - PQR - Euclid
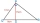 Find the length of line segment PR - leg of the right triangle PQR. PQ=17 cm PS=15 cm QS=8 cm; Point S is the height touch point with a hypotenuse of the RQ.
Find the length of line segment PR - leg of the right triangle PQR. PQ=17 cm PS=15 cm QS=8 cm; Point S is the height touch point with a hypotenuse of the RQ. - Find area 2
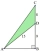 Find the area of the green region in the given picture. Dimensions are shown.
Find the area of the green region in the given picture. Dimensions are shown.
- Smaller square
 Let the points A, B, C and D are midpoints of the sides of the square PQRS. If the area of PQRS is 100 sq cm, what is the area of the smaller square ABCD?
Let the points A, B, C and D are midpoints of the sides of the square PQRS. If the area of PQRS is 100 sq cm, what is the area of the smaller square ABCD? - Parallelogram - right angles
 In parallelogram ABCD; AB = 16 cm, BC = 12 cm and diagonal AC = 20 cm. Find the area of the parallelogram.
In parallelogram ABCD; AB = 16 cm, BC = 12 cm and diagonal AC = 20 cm. Find the area of the parallelogram. - Circle inscribed square
 What is the area of the circle that can be inscribed in a square of 10 cm?
What is the area of the circle that can be inscribed in a square of 10 cm? - ET inscribed circle
 An equilateral triangle has been inscribed in a circle with a radius of 4 cm . Find the area of the shaded region.
An equilateral triangle has been inscribed in a circle with a radius of 4 cm . Find the area of the shaded region. - Cuboid - sum of edges length
 Calculate the cuboid's dimensions if the sum of its edges is 19 cm. The body's diagonal size is 13 cm, and its volume is 144 cm³. The total surface area is 192 cm².
Calculate the cuboid's dimensions if the sum of its edges is 19 cm. The body's diagonal size is 13 cm, and its volume is 144 cm³. The total surface area is 192 cm². - A frustum
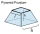 A frustum of a pyramid consists of a square base of length 10 cm and a top square of length 7 cm. The height of the frustum is 6 cm. Calculate the surface area and volume.
A frustum of a pyramid consists of a square base of length 10 cm and a top square of length 7 cm. The height of the frustum is 6 cm. Calculate the surface area and volume. - A lamp
 A lamp shade like that of a frustum has a height of 12 cm and an upper and lower diameter of 10 cm and 20 cm. What area of materials is required to cover the curved surface of the frustum?
A lamp shade like that of a frustum has a height of 12 cm and an upper and lower diameter of 10 cm and 20 cm. What area of materials is required to cover the curved surface of the frustum? - 216 surface area and volume
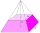 Calculate the surface area and volume of a regular tetrahedral pyramid: a = 6 cm and the body height is 12 cm.
Calculate the surface area and volume of a regular tetrahedral pyramid: a = 6 cm and the body height is 12 cm.
- 4B - truncated pyramid
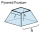 Calculate the volume of a regular truncated quadrilateral pyramid if the base edges are 10cm and 4cm and the height of the side wall is 5cm.
Calculate the volume of a regular truncated quadrilateral pyramid if the base edges are 10cm and 4cm and the height of the side wall is 5cm. - Legs and ratio
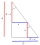 For the legs of a right triangle, a : b = 6:8. The hypotenuse has a length of 61 cm. Calculate the perimeter and area of this triangle.
For the legs of a right triangle, a : b = 6:8. The hypotenuse has a length of 61 cm. Calculate the perimeter and area of this triangle. - RRL Basics
 What is the length of the smaller base of an isosceles trapezoid and the height, if a = 9 dm, the side is 6 dm and the angle ACB is 90 degrees?
What is the length of the smaller base of an isosceles trapezoid and the height, if a = 9 dm, the side is 6 dm and the angle ACB is 90 degrees? - Base RR odd
 The base of the prism is an isosceles trapezoid ABCD with bases AB = 12 cm, and CD = 9 cm. The angle at vertex B is 48° 10'. Determine the volume and area of the prism if its height is 35 cm.
The base of the prism is an isosceles trapezoid ABCD with bases AB = 12 cm, and CD = 9 cm. The angle at vertex B is 48° 10'. Determine the volume and area of the prism if its height is 35 cm. - Calculate
 A rotating cone has a diameter of 16 cm and a side of 10 cm. Calculate the surface area and volume of the solid.
A rotating cone has a diameter of 16 cm and a side of 10 cm. Calculate the surface area and volume of the solid.
Do you have unsolved problem that you need help? Ask a question, and we will try to solve it. Solving math problems.
The Pythagorean theorem is the base for the right triangle calculator. Area - practice problems. Pythagorean theorem - practice problems.
