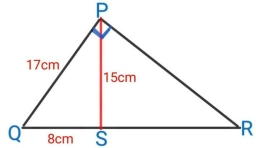
PQR - Euclid
Find the length of line segment PR - leg of the right triangle PQR.
PQ=17 cm
PS=15 cm
QS=8 cm;
Point S is the height touch point with a hypotenuse of the RQ.
PQ=17 cm
PS=15 cm
QS=8 cm;
Point S is the height touch point with a hypotenuse of the RQ.
Final Answer:
Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
geometryalgebraarithmeticplanimetricsUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- Rectangular triangle PQR
In the rectangular triangle PQR, the PQ leg is divided by the X point into two segments, of which longer is 25cm long. The second leg PR has a length of 16 cm. The length of the RX is 20 cm. Calculate the length p of side RQ. The result is round to 2 deci - Karim
Karim uses a photocopier to enlarge the triangle PQR diagram by 150%. a) Write the ratio of the length of P' Q' to the length of PQ. b) Is the ratio of the length P 'R' to the length PR equal to the ratio of the length P 'Q' to the length PQ? c) Use your - Points OPQ
Point P is on line segment OQ. Given OP = 6, OQ = 4x - 3, and PQ = 3x, find the numerical length of OQ. - Triangle KLM
In the rectangular triangle KLM, where |KL|=m is the hypotenuse (sketch it!). Find the length of the leg k and the height of triangle h if the hypotenuse's segments are known MK = 5cm and ml = 15 cm. - Points on line segment
Points P and Q belong to segment AB. If AB=a, AP = 2PQ = 2QB, find the distance between point A and the midpoint of segment QB. - Number axis point
On the number axis, point P is the image of the number -2.54, and point Q is the image of the number 10.71. Find which number is the point R such that Q is the center of the line PR. - MIT 1869
You know the length of parts 9 and 16 of the hypotenuse, at which a right triangle's hypotenuse is divided by a height. The task is to find the lengths of the sides of the triangle and the length of line x. This assignment was part of the Massachusetts In
