Rectangular triangle PQR
In the rectangular triangle PQR, the PQ leg is divided by the X point into two segments, of which longer is 25cm long. The second leg PR has a length of 16 cm. The length of the RX is 20 cm. Calculate the length p of side RQ. The result is round to 2 decimal places. Units "cm"
Correct answer:
Tips for related online calculators
Do you want to convert length units?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
- algebra
- expression of a variable from the formula
- planimetrics
- Pythagorean theorem
- right triangle
- triangle
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- PQR - Euclid
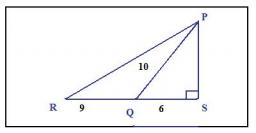
Find the length of line segment PR - leg of the right triangle PQR. PQ=17 cm PS=15 cm QS=8 cm; Point S is the height touch point with a hypotenuse of the RQ. - Karim
Karim uses a photocopier to enlarge the triangle PQR diagram by 150%. a) Write the ratio of the length of P' Q' to the length of PQ. b) Is the ratio of the length P 'R' to the length PR equal to the ratio of the length P 'Q' to the length PQ? c) Use your - Rectangular 44951
The surface area of the rectangular plot needs to be increased by 33.7 percent. One dimension was extended by 2.9 percent. By what percentage should the second dimension be increased? Round the result to two decimal places. - Trapezoid 7537
Diagonal alpha equals 0.4 m, and diagonal beta equals 0.4 m in the isosceles trapezoid. Side AB is 120 cm, and side DC is 7.6 dm. Find the length of arms in an isosceles trapezoid. Please result round to 2 decimal places.
- Calculating 63344
Calculate the volume of the cone formed by rotating an isosceles triangle about the height of the base. The triangle has a side length of 15 cm and a height to the base of 12 cm. When calculating, use the value pi = 3.14 and round the result to one decima - Measuring 65374
Calculate the length of the body diagonal of a block measuring 6 cm, 7 cm, and 10 cm, and round the result to two decimal places. - Triangle KLM
In the rectangular triangle KLM, where |KL|=m is the hypotenuse (sketch it!). Find the length of the leg k and the height of triangle h if the hypotenuse's segments are known MK = 5cm and ml = 15 cm.
