Points OPQ
Point P is on line segment OQ. Given OP = 6, OQ = 4x - 3, and PQ = 3x, find the numerical length of OQ.
Correct answer:
Showing 1 comment:
Tips for related online calculators
Do you have a linear equation or system of equations and are looking for its solution? Or do you have a quadratic equation?
Do you want to convert length units?
Do you want to convert length units?
You need to know the following knowledge to solve this word math problem:
geometryalgebraUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- Line segments
There are three line segments on the line: the length of MN = 3 1/2, the length of NO= 2 3/4, and the length of OP=1 2/3. Find the length of line segment MP. Write your answer as a mixed number. - Points on line segment
Points P and Q belong to segment AB. If AB=a, AP = 2PQ = 2QB, find the distance between point A and the midpoint of segment QB. - PQR - Euclid
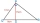Find the length of line segment PR - leg of the right triangle PQR. PQ=17 cm PS=15 cm QS=8 cm; Point S is the height touch point with a hypotenuse of the RQ. - Midpoint 6
For line segment length is given: FM=8a+1, FG=42. Point M is the midpoint of FG. Find unknown a. - The midpoint 2
Find the value of x if M is the midpoint of PQ, PQ=10x−7, and PM=14. - Belongs 8412
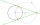Given a circle k(O; 2.5 cm), a line p: /Op/=4 cm, a point T: T belongs to p and at the same time /OT/=4.5 cm. We must find all the circles that will touch the circle k and the line p at point T. - Midpoint 5 FM=3x-4, MG=5x-26, FG=? Point M is the midpoint of FG. Use the given information to find the unknown measure or value.
