Equations practice problems
An equation is a statement that asserts the equality of two expressions, which are connected by the equals sign =. Solving an equation containing variables consists of determining which values of the variables make the equality true. The variables for which the equation has to be solved are also called unknowns, and the values of the unknowns that satisfy the equality are called solutions of the equation.Number of problems found: 4535
- Two types of ore
A total of 42 tons of two types of ore is to be added into a smelter. The first type contains 6% copper and the other contains 2.5% copper. Find the necessary amounts of each ore to produce 2 tons of copper. - The average 19
The average age of a class was 15 years. When 5 boys whose average age was 12 years 6 months were admitted in the class, the average was reduced by 6 months. How many students were there in the class originally? - The shadow 2
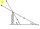The shadow of a tower standing on a level ground is found to be 40 m longer when the Sun’s altitude is 30° than when it is 60°. Find the height of the tower. - Journey trip
A man performs 2/15 of the total journey by rail, 9/20 by bus and the remaining 10 km, on the cycle. What is his total journey?
- Goods train
A goods train runs at the speed of 72 kmph and crosses a 250 m long platform in 26 seconds. What is the length of the goods train? - Last Friday
3/4 of the children were present at school last Friday. If there are 90 children present, how many children were absent? - Digits sum
A two digit number is 3 times the sum of its digits. If 45 is added to the number, its digits are interchanged. Find the sum of the digits of the number. - The sum 52 The sum of digits of a two digits number is 10. On interchanging the digit, the number obtained is 54 less than the original number. What is the original number?
- The ratio 21
The ratio between the number of sides of two regular polygon is 1:2 and ratio of sum of their interior angles is 2:3. Find their number of sides.
- Two friends 5 Two friends, X and Y. X is 36 years old and Y is 16 years. In how many years X will be twice as old as Y?
- The ages 3 The ages of A and B are in ratio of 5:4. Three years hence the ratio of their ages will become 11:9. What is the present age of B?
- A rectangle 15
A rectangle is 5 cm longer its width. It areas is 6 cm square. What are the dimensions of the rectangle. - Subtracting 7
Subtracting 50 from 50% of a number we get 50 as remainder. Find the number. - A man 24
A man distributed 25300 EUR among his 3 sons A, B, C in such a way that the amounts of their parts at 10% simple interest in 2 years, 3 years, 4 years will be equal. A's share?
- Train station
A man walks from his house to station. If he walks at 5 km/h he misses a train by 7 minutes. However, if he walks at 6 km/h, he reaches the station 5 minutes before the departure of the train. Find the distance covered by him to reach the station. - Two masons Mason A can build a wall in 30 days, while mason B can build it in 40 days. If they build it together and get a payment of USD 7000, what is B's share?
- The length 20
The length and breadth of a rectangular park are in the ratio 8:5. A path,1.5 m wide, running all around the outside of the park has an area of 594 sq m. Find the dimensions of the park. - A field
A field is in the shape of a trapezium whose parallel sides are 25 m and 10 m and the non parallel sides are 14 m and 13 m. Find the area of the field. - The average 17
The average monthly salary of 20 workers in an office is $4590 . If the manage's salary is added, the average salary becomes $ 4920 per month What's the manager's monthly salary?
The product of two consecutive natural numbers which are multiples of 3 is equal to 810. Find the two numbers.Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
