Příklady na rovnice
Rovnice je výrok, rovnost dvou výrazů, které jsou spojeny znakem rovnosti =. Řešení rovnice obsahující proměnné sestává z určení, které hodnoty proměnných činí rovnost pravdivou. Proměnné, pro které musí být rovnice vyřešena, se také nazývají neznámé. Hodnoty neznámých, které splňují rovnost, se nazývají řešení rovnice.Počet nalezených příkladů: 4439
- MDZ - divadlo
 V divadle je 798 mužů, žen a dětí. Počet mužů je dvojnásobný počtu žen. Počet žen je dvojnásobný počtu dětí. Kolik bylo mužů, žen a dětí?
V divadle je 798 mužů, žen a dětí. Počet mužů je dvojnásobný počtu žen. Počet žen je dvojnásobný počtu dětí. Kolik bylo mužů, žen a dětí? - Ve středu 2
 Ve středu mezi neznámým číslem a číslem 30 je číslo 12. Urči neznámé číslo.
Ve středu mezi neznámým číslem a číslem 30 je číslo 12. Urči neznámé číslo. - Řešte R
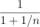 Řešte rovnici se závorkami: 5×(2u-9)-8×(0,5-3u)=4×(7u-1)-3
Řešte rovnici se závorkami: 5×(2u-9)-8×(0,5-3u)=4×(7u-1)-3 - Kolik 147
 Kolik po sobě jdoucích přirozených čísel od 1 do n musíte nejméně sečíst, aby jejich součet přesáhl 1000000?
Kolik po sobě jdoucích přirozených čísel od 1 do n musíte nejméně sečíst, aby jejich součet přesáhl 1000000? - Čtvrtina 10
 Čtvrtina neznámého čísla zvětšená o sto je padesát. Jaké je neznámé číslo?
Čtvrtina neznámého čísla zvětšená o sto je padesát. Jaké je neznámé číslo? - Vypočítejte 249
 Vypočítejte objem válce, je-li dáno: S = 144pí cm² výška = 6 cm
Vypočítejte objem válce, je-li dáno: S = 144pí cm² výška = 6 cm - Směnka prodej
 Podnikatel koupil směnku 6 měsíců před lhůtou splatnosti. Po odečtení úroku při úrokové míře 10% p. . a. zaplatil za ni 19 000 €. Kolik € úroku se odečítalo z nominální hodnoty směnky?
Podnikatel koupil směnku 6 měsíců před lhůtou splatnosti. Po odečtení úroku při úrokové míře 10% p. . a. zaplatil za ni 19 000 €. Kolik € úroku se odečítalo z nominální hodnoty směnky? - Traktor 19
 Traktor zorá pole za 48 hodin s použitím pluhu s 5 radlicemi. Jak dlouho mu bude trvat orba téhož pole s pluhem se 6 stejně širokými radlicemi při nezměněné rychlosti traktoru?
Traktor zorá pole za 48 hodin s použitím pluhu s 5 radlicemi. Jak dlouho mu bude trvat orba téhož pole s pluhem se 6 stejně širokými radlicemi při nezměněné rychlosti traktoru? - Jana a Tomáš
 Jana a Tomáš dostali dohromady od babičky 105 Kč. Jana dostala o třetinu více než Tomáš. O kolik Kč dostal Tomáš méně než Jana?
Jana a Tomáš dostali dohromady od babičky 105 Kč. Jana dostala o třetinu více než Tomáš. O kolik Kč dostal Tomáš méně než Jana? - Trávova směs
 Peter plánuje nakoupit trávovou směs složenou ze semene lipnice a kostřavy za 40 eur. 1 kg lipnice stojí 6 eur a 1 kg kostřavy stojí 10 eur. Kolik které složky má koupit, má-li výsledná směs mít hmotnost 6kg?
Peter plánuje nakoupit trávovou směs složenou ze semene lipnice a kostřavy za 40 eur. 1 kg lipnice stojí 6 eur a 1 kg kostřavy stojí 10 eur. Kolik které složky má koupit, má-li výsledná směs mít hmotnost 6kg? - Oplátka, tyčinka
 Jarmila si koupila oplátku, tyčinku a čokoládu. Zaplatila 38 Kč. Tyčinka byla o 8 Kč dražší než oplatka, čokoláda je čtyřikrát dražší než oplatka. Kolik stála oplatka, tyčinka a čokoláda?
Jarmila si koupila oplátku, tyčinku a čokoládu. Zaplatila 38 Kč. Tyčinka byla o 8 Kč dražší než oplatka, čokoláda je čtyřikrát dražší než oplatka. Kolik stála oplatka, tyčinka a čokoláda? - Fyzikus - deska, páka
 Na stole je položena dřevěná deska o hmotnosti 0,5 kg. O jakou část své délky může přečnívat přes okraj stolu, aby nespadla, leží-li na jejím konci závaží o hmotnosti 0,2 kg?
Na stole je položena dřevěná deska o hmotnosti 0,5 kg. O jakou část své délky může přečnívat přes okraj stolu, aby nespadla, leží-li na jejím konci závaží o hmotnosti 0,2 kg? - GP - volná
 Pro geometrickou posloupnost platí zajímavý vztah mezi prvním a třetím členem: a1-a3=-1,5 a3-a1=1,5 Vypočítejte kvocient q a první člen a1.
Pro geometrickou posloupnost platí zajímavý vztah mezi prvním a třetím členem: a1-a3=-1,5 a3-a1=1,5 Vypočítejte kvocient q a první člen a1. - Hůlky - čaroděj
 Čislice slíbila kouzelníkovi Rododendrovi, že ho hodně naučí o číslech, ale musí vyřešit její hádanku: Moje dvě kouzelné hůlky spolu měří 63 cm. Jeden je delší o 7 cm. Kolik měří její hůlky?
Čislice slíbila kouzelníkovi Rododendrovi, že ho hodně naučí o číslech, ale musí vyřešit její hádanku: Moje dvě kouzelné hůlky spolu měří 63 cm. Jeden je delší o 7 cm. Kolik měří její hůlky? - Rovnost momentů
 Páka o hmotnosti 3 kg a délce 2 m je zatížena na konci závažími o hmotnosti 5 kg a 8 kg. Najděte místo, kde je třeba páku podepřít, aby byla v rovnováze.
Páka o hmotnosti 3 kg a délce 2 m je zatížena na konci závažími o hmotnosti 5 kg a 8 kg. Najděte místo, kde je třeba páku podepřít, aby byla v rovnováze. - Já a táta
 Já a otec máme dnes spolu 55 let. Když budeme mít spolu 65 let, bude otec čtyřikrát starší než já. Kolik je mi let?
Já a otec máme dnes spolu 55 let. Když budeme mít spolu 65 let, bude otec čtyřikrát starší než já. Kolik je mi let? - Ořechy 8
 Peter rozdělil ořechy dvěma kamarádům. Každý z kamarádů dostal čtvrtinu všech ořechů a ještě dva ořechy zůstaly.
Peter rozdělil ořechy dvěma kamarádům. Každý z kamarádů dostal čtvrtinu všech ořechů a ještě dva ořechy zůstaly. - Daniel 3
 Daniel a Eva spolu vydělali 180 eur. Daniel vydělal o 70 eur více než Eva. Kolik vydělal Daniel a kolik Eva?
Daniel a Eva spolu vydělali 180 eur. Daniel vydělal o 70 eur více než Eva. Kolik vydělal Daniel a kolik Eva? - Tři kamarádi 10
 Tři kamarádi Petr, Tomáš a Jirka si vydělali na brigádě 4000Kč. Petr si vydělal třikrát více než Tomáš a Jirka o 500 Kc více než Tomáš. Kolik vydělal každý z nich?
Tři kamarádi Petr, Tomáš a Jirka si vydělali na brigádě 4000Kč. Petr si vydělal třikrát více než Tomáš a Jirka o 500 Kc více než Tomáš. Kolik vydělal každý z nich? - Matěj 2
 Matej, Marko, Milan Matúš měli spolu 205 karticek fotbalistů is podpisy. Marko má čtyřikrát více než Matěj. Matouš měl dvakrát méně než Marko. Milan měl o 20 karticek méně než Matouš. Kolik karticek měl každý?
Matej, Marko, Milan Matúš měli spolu 205 karticek fotbalistů is podpisy. Marko má čtyřikrát více než Matěj. Matouš měl dvakrát méně než Marko. Milan měl o 20 karticek méně než Matouš. Kolik karticek měl každý?
Máš příklad z matematiky, který jsi tady nenašel vyřešený? Pošli nám příklad a my Ti ho zkusíme vypočítat.
