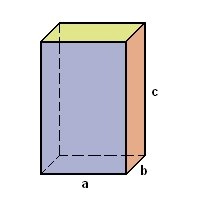
Cuboid - sum of edges length

Calculate the cuboid's dimensions if the sum of its edges is 19 cm. The body's diagonal size is 13 cm, and its volume is 144 cm3. The total surface area is 192 cm2.

Final Answer:

a =  3 cm
b =  4 cm
c =  12 cm

Step-by-step explanation:

d=13 cm V=144 cm3  a+b+c=19 a2+b2+c2 = d2 = 132 V=abc 144 = 2 × 2 × 2 × 2 × 3 × 3 = 24 × 32 192 = 2 × 2 × 2 × 2 × 2 × 2 × 3 = 26 × 3  a=3=3 cm  A=V/a=144/3=48 cm2 A=48 = 2 × 2 × 2 × 2 × 3 = 24 × 3  b=22=4 cm c=22⋅ 3=12 cm   Verifying Solution:  S1​=2⋅ (a⋅ b+b⋅ c+c⋅ a)=2⋅ (3⋅ 4+4⋅ 12+12⋅ 3)=192 cm2 V1​=a⋅ b⋅ c=3⋅ 4⋅ 12=144 cm3 d1​=a2+b2+c2​=32+42+122​=13 cm s1​=a+b+c=3+4+12=19 cm

Try another example


Did you find an error or inaccuracy? Feel free to send us. Thank you!







Tips for related online calculators
Do you have a system of equations and are looking for calculator system of linear equations?
Do you solve Diofant problems and are looking for a calculator of Diofant integer equations?
Tip: Our volume units converter will help you convert volume units.
The Pythagorean theorem is the base for the right triangle calculator.

You need to know the following knowledge to solve this word math problem:

algebraarithmeticsolid geometryplanimetricsUnits of physical quantitiesGrade of the word problem

 
We encourage you to watch this tutorial video on this math problem: video1   video2

Related math problems and questions: