Cuboid practice problems
A cuboid is a three-dimensional shape with a length, width, and height. A cuboid is a Rectangular Prism. The cuboid body has six sides called faces. Each face of a cuboid is a rectangle, and all of a cuboid's corners (called vertices) are 90-degree angles. Opposite faces are parallel. A cuboid has the shape of a rectangular box.Number of problems found: 758
- Water tank 12
A rectangular water tank is 5 m high, 3 m long, and 2 m wide. How many liters of water can it hold? - Box/cuboid
What is the volume of a box with these dimensions: H = 1.5 dm W = 3.5 dm L = 45 cm Give your answer in dm³ and round to the nearest tenth. - A rectangular 9
A rectangular tank measuring 50 cm by 54 cm by 40 cm is 3/5 filled with water. 21.6L of the water is removed. What is the volume of water left in the tank? Give your answer in liters. - A water 2 A water tank is 2m long, 1.9m wide, and 964 mm deep. How much water will it hold? Answer in liters. 2nd question: A tank that is 2.5 m long and 1.5m deep holds 6.75 cubic meters of water. What is its width?
- Cuboid - sum of edges length Calculate the cuboid's dimensions if the sum of its edges is 19 cm. The body's diagonal size is 13 cm, and its volume is 144 cm³. The total surface area is 192 cm².
- Height of the box The box needs to have a volume of 108 ¾ cubic inches. If its width is 7 ¼ inches and its depth is 1 ¼ inches, what must its height be?
- The volume 9 The volume of a large tank is 210 yd³. It is 2 2/5 yd wide and 2 4/5 yd high. What is the length of the tank?
- The cuboid 2
If the areas of three adjacent faces of a cuboid are 6,10,22 respectively then find the volume of the cuboid. - Water 66 Water flows from a tap into a rectangular tank that measures 64cm by 36cm by 45cm. At 8 p. m., it is 1/4 filled with water. At 9 p. m., it is filled with 69,120 cm³ of water. Find the volume of water that has flowed into the tank from 8 p. m. to 9 p. m. G
- Tomato plant
Bruce's grandmother loves to use fresh tomatoes in her homemade pasta sauce. Bruce thought she might like to grow her own, so he bought her a planter box and a tomato plant. The planter box is shaped like a rectangular prism. It is 12 1/2 inches long, 10 - Plasticine cuboid
Paul makes a cuboid of plasticine with sides 5 cm, 2 cm, and 5 cm. How many such cuboids will he need to form a cube? - The size 3 The size of a wooden block is 15cm × 12cm × 20cm. How many such blocks will be required to construct a solid wooden cube of minimum size?
- Saria
Saria is wrapping a gift for her mother. The gift box is in the shape of a rectangular prism and is 5 centimeters high, 25 centimeters long, and 40 centimeters wide. How much wrapping paper will you need to wrap the gift box? - Two cubes 2 Two cubes each of volume 125 cm³ are joined end to end. Find the surface area of the resulting cuboid .
- Spire - prism Calculate the surface of a spire with a base in the shape of a rectangle with dimensions of 5m and 6m. The height of the spire is 7m.
- Building blocks Rosa bought a set of building blocks for her younger brother, Owen, for his birthday. Owen opened the gift and immediately used all 35 blocks in the set to build a tower shaped like a rectangular prism. Each block is a cube that is 1 1/2 inches along each
- Toy Store Beezlebum's Toy Store can't keep its stackable block set in stock! The blocks completely fill a box shaped like a rectangular prism that is 14 inches long, 14 inches wide, and 21 inches tall. The cube-shaped blocks in the set are 3.5 inches along each edg
- Storage shed
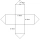Frank designed a net for a storage shed that he is going to construct out of metal. The design consists of a square base and four square sides, plus four triangular parts that make up the roof. A square base of 6 feet and four square sides, plus 4 feet of - Two cuboids
Find the volume of the cuboidal box with one edge: a) 1.4m and b) 2.1 dm. - How much 4
How much juice is needed to fill a glass that is 9 m deep and 5 m wide, and 12 m long?
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
