Volume of three cuboids
Calculate the total volume of all cuboids for which the edges' sizes are in a ratio of 1:2:3, and one of the edges has a size of 6 cm.
Final Answer:
Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
arithmeticsolid geometrybasic operations and conceptsUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- Cuboid - sum of edges length
 Calculate the cuboid's dimensions if the sum of its edges is 19 cm. The body's diagonal size is 13 cm, and its volume is 144 cm³. The total surface area is 192 cm².
Calculate the cuboid's dimensions if the sum of its edges is 19 cm. The body's diagonal size is 13 cm, and its volume is 144 cm³. The total surface area is 192 cm². - Cuboid - ratios
 The sizes of the edges of the cuboid are in the ratio of 2:3:5. The smallest wall has an area of 54 cm². Calculate the surface area and volume of this cuboid.
The sizes of the edges of the cuboid are in the ratio of 2:3:5. The smallest wall has an area of 54 cm². Calculate the surface area and volume of this cuboid. - Two cuboids
 The cuboid has dimensions of 2m 3m 4m We increase the length of all edges by 50 cm. 1. Calculate in % how much the surface area of the cuboid increases compared to the surface area of the original cuboid - round the result to whole percent 2. Calculat
The cuboid has dimensions of 2m 3m 4m We increase the length of all edges by 50 cm. 1. Calculate in % how much the surface area of the cuboid increases compared to the surface area of the original cuboid - round the result to whole percent 2. Calculat - Cubes - diff
 The second cube's edge is 2 cm longer than the edge of the first cube. Volume difference blocks are 728 cm³. Calculate the sizes of the edges of the two dice.
The second cube's edge is 2 cm longer than the edge of the first cube. Volume difference blocks are 728 cm³. Calculate the sizes of the edges of the two dice. - Nice prism
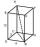 Calculate the cuboid's surface if the sum of its edges is a + b + c = 19 cm and the body diagonal size u = 13 cm.
Calculate the cuboid's surface if the sum of its edges is a + b + c = 19 cm and the body diagonal size u = 13 cm. - Cuboid face diagonals
 The lengths of the cuboid edges are in the ratio 1:2:3. Will the lengths of its diagonals be in the same ratio? The cuboid has dimensions of 5 cm, 10 cm, and 15 cm. Calculate the size of the wall diagonals of this cuboid.
The lengths of the cuboid edges are in the ratio 1:2:3. Will the lengths of its diagonals be in the same ratio? The cuboid has dimensions of 5 cm, 10 cm, and 15 cm. Calculate the size of the wall diagonals of this cuboid. - Quadrilateral 42151
 Calculations from geometry: The ratios of the sides of the quadrilateral are 3 : 6:4.5 : 3.5. Calculate their lengths if the circumference is 51 cm. The sizes of the angles in the quadrilateral are equal to 29°30', 133°10', and 165°20'. What is the size o
Calculations from geometry: The ratios of the sides of the quadrilateral are 3 : 6:4.5 : 3.5. Calculate their lengths if the circumference is 51 cm. The sizes of the angles in the quadrilateral are equal to 29°30', 133°10', and 165°20'. What is the size o
