Cuboid - ratios
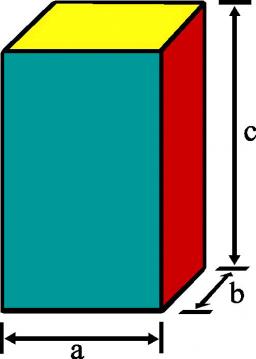
The sizes of the edges of the cuboid are in the ratio of 2:3:5. The smallest wall has an area of 54 cm2. Calculate the surface area and volume of this cuboid.
Your answer:
Your answer:
Tips for related online calculators
Are you looking for help with calculating roots of a quadratic equation?
Check out our ratio calculator.
Tip: Our volume units converter will help you convert volume units.
Check out our ratio calculator.
Tip: Our volume units converter will help you convert volume units.
You need to know the following knowledge to solve this word math problem:
algebraarithmeticsolid geometryplanimetrybasic operations and conceptsUnits of physical quantitiesGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Cuboid edges
Calculate the volume and surface of a cuboid whose edge lengths are in the ratio 2:3:4 and the longest edge measures 10 cm. - Block or cuboid
The wall diagonals of the block have sizes of √29 cm, √34 cm, and √13 cm. Calculate the surface and volume of the block. - Block Edges from Volume
The block volume is 900 cm3, and the surface is 600 cm². The area of one wall is 60 cm². Calculate the length of edges a, b, and c. - Cuboid surface ratio
The volume of the cuboid is 960 cm³. The lengths of the edges are in the ratio 1 : 3: 5. Calculate the surface area of the cuboid. - Ratio-cuboid
The edges of a cuboid are in the ratio 2:3:6. Its space diagonal is 14 cm long. Calculate the volume and surface area of the cuboid. - Block surface ratio The volume of the block is 7,500 dm³. The lengths of the edges are in the ratio 3: 4: 5. Calculate the surface area of the cuboid.
- Cuboid face diagonals
The lengths of the cuboid edges are in the ratio 1:2:3. Will the lengths of its diagonals be in the same ratio? The cuboid has dimensions of 5 cm, 10 cm, and 15 cm. Calculate the size of the wall diagonals of this cuboid.
