Ratio - practice problems
Ratio problems are word problems that use ratios to relate the different items in the question. On solving problems and tasks proportionally, we recommend a hint rule of three. Rule of three (proportionality) helps solve examples of direct and inverse proportionality. Three members make it possible to calculate the fourth - unknown member. Ratio and proportion.Number of problems found: 1617
- Three in a ratio
If A is 40% more than B, B is 20% less than C then, find the ratio A : C. - School - boys:girls
In a school 10% of boy is equal to the 1/4 of number of girls and 10% of the number of girls is equal to the 1/25 of boys. Find the ratio between the number of boys and girls. - Compare ratios Is ratios 4:7 and 16:19 equivalent?
- Alcohol mixture 3
A mixture contains alcohol and water in the ratio 4:3. If 7 liters of water is added, the ratio of alcohol and water becomes 3:4. Find the quantity of alcohol in the mixture. - A person 3
A person distributes his pens among four friends A, B, C and D in the ratio 1/3 : 1/4 : 1/5 : 1/6. What is the minimum number of pens that the person should have? - The Earth and Moon
The diameter of the Moon is approximately 1/4 of the diameter of the Earth. What fraction of the volume of the Earth is the volume of the Moon? - Salaries - ratio3
The salaries A, B, C are in the ratio 2 : 3 : 5. If the increments of 15%, 10% and 20% are allowed respectively in their salaries, then what will be new ratio of their salaries?
- Angle of inclination
Find the angle of inclination of a ramp that rise for 80 cm and is 200 cm long. - The ratio 21
The ratio between the number of sides of two regular polygon is 1:2 and ratio of sum of their interior angles is 2:3. Find their number of sides. - The ages 3 The ages of A and B are in ratio of 5:4. Three years hence the ratio of their ages will become 11:9. What is the present age of B?
- The length 20
The length and breadth of a rectangular park are in the ratio 8:5. A path,1.5 m wide, running all around the outside of the park has an area of 594 sq m. Find the dimensions of the park. - Four numbers 3
What least number must be added to each of the numbers 6,15,20 and 43 to make them proportional? - Collecting money
Rs 180 contained in a box of one rupee, 50 Paise and 25 Paise coins in the ratio 2:3:4. What is the number of 50 Paise coins? (One rupee = 100 paisa) - Percents and ratio When 20% of a number is added to another number, the number increases by 50%. What is the ratio of the two numbers?
- Three inscribed objects
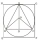A circle is inscribed in a square. An equilateral triangle of side 4√3 is inscribed in that circle. Find the length of the diagonal of the square.
- Sharing money 2
Ann and Betty shared a sum of money in the ratio is 2:3 and Ann received $120. What is Betty share? - Children ratio
In a certain office 1/3 of the workers are women,1/2 of the women are married and 1/3 of the married women have children. If 3/4 of the men are married and 2/3 of the married men have children, what part of the workers is without children? - Scholarship 3
The ratio of number of boys to that of the girls in a school is 3:2. If 20% of boys and 25% of the girls are scholarship holders, find the percentage of those who are not scholarship holders? - Shares 1300 USD are divided among A, B, C and D in such a way that: share of (A/B)=(B/C)=(C/D) = (2/3)
- Spheres - ratios
The surface area of two spheres are in the ratio 1 : 4 . Find the ratio of their volumes.
Do you have unsolved problem that you need help? Ask a question, and we will try to solve it. Solving math problems.
Check out our ratio calculator.
