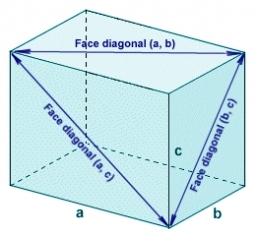
Cuboid face diagonals
The lengths of the cuboid edges are in the ratio 1:2:3. Will the lengths of its diagonals be in the same ratio?
The cuboid has dimensions of 5 cm, 10 cm, and 15 cm. Calculate the size of the wall diagonals of this cuboid.
Result
The cuboid has dimensions of 5 cm, 10 cm, and 15 cm. Calculate the size of the wall diagonals of this cuboid.
Result
Tips for related online calculators
Check out our ratio calculator.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
Related math problems and questions:
- The block
The block has dimensions of 5 cm, 10 cm, and 15 cm. Calculate the size of the wall diagonals of this block. - Cuboid diagonals
The cuboid has dimensions of 15, 20, and 40 cm. Calculate its volume and surface, the length of the body diagonal, and the lengths of all three wall diagonals. - Cuboid and ratio
A cuboid has a volume of 810 cm³. The lengths of edges from the same vertex are in a ratio of 2:3:5. Find the dimensions of a cuboid. - Cuboid - ratios
The sizes of the edges of the cuboid are in the ratio of 2:3:5. The smallest wall has an area of 54 cm². Calculate the surface area and volume of this cuboid.
- Wall and body diagonals
Calculate the lengths of the wall and body diagonals of the cuboid with edge dimensions of 0.5 m, 1 m, and 2 m - Cuboid edges
Calculate the volume and surface of a cuboid whose edge lengths are in the ratio 2:3:4 and the longest edge measures 10cm. - Volume of three cuboids
Calculate the total volume of all cuboids for which the edges' sizes are in a ratio of 1:2:3, and one of the edges has a size of 6 cm.
