Prism practice problems
A prism is a polyhedron comprising an n-sided polygonal base, a second base which is a translated copy (rigidly moved without rotation) of the first, and n other faces (necessarily all parallelograms) joining corresponding sides of the two bases. All cross-sections parallel to the bases are translations of the bases. Prisms are named for their bases, so a prism with a pentagonal base is called a pentagonal prism.Number of problems found: 550
- Eva wraps
Eva wraps a gift box in the shape of a right rectangular prism. The figure shows a net for the gift box. How much wrapping paper did she use, in square meters? - Prism - base and height
Find volume of the prism if the base area equals 20 inches² with the height is 12 inches. - A triangular prism
Find the number of faces, edges, and vertices of a triangular prism. - Water 66
Water flows from a tap into a rectangular tank that measures 64cm by 36cm by 45cm. At 8 p. m., it is 1/4 filled with water. At 9 p. m., it is filled with 69,120 cm³ of water. Find the volume of water that has flowed into the tank from 8 p. m. to 9 p. m. G - Tomato plant
Bruce's grandmother loves to use fresh tomatoes in her homemade pasta sauce. Bruce thought she might like to grow her own, so he bought her a planter box and a tomato plant. The planter box is shaped like a rectangular prism. It is 12 1/2 inches long, 10 - Saria
Saria is wrapping a gift for her mother. The gift box is in the shape of a rectangular prism and is 5 centimeters high, 25 centimeters long, and 40 centimeters wide. How much wrapping paper will you need to wrap the gift box? - Spire - prism
Calculate the surface of a spire with a base in the shape of a rectangle with dimensions of 5m and 6m. The height of the spire is 7m.
- The volume 8
The volume of a right regular hexagonal prism is 187.2 cubic millimeters. The line segment that has a length of 2.6 millimeters begins at the center of the hexagon and ends at one side of the hexagon. 3 mm base. Find the height. - Building blocks
Rosa bought a set of building blocks for her younger brother, Owen, for his birthday. Owen opened the gift and immediately used all 35 blocks in the set to build a tower shaped like a rectangular prism. Each block is a cube that is 1 1/2 inches along each - Toy Store Beezlebum's Toy Store can't keep its stackable block set in stock! The blocks completely fill a box shaped like a rectangular prism that is 14 inches long, 14 inches wide, and 21 inches tall. The cube-shaped blocks in the set are 3.5 inches along each edg
- Storage shed
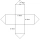Frank designed a net for a storage shed that he is going to construct out of metal. The design consists of a square base and four square sides, plus four triangular parts that make up the roof. A square base of 6 feet and four square sides, plus 4 feet of - A rectangular prism
A gift box in the shape of a rectangular prism measures 8 by 10 inches. What is the least amount of wrapping paper needed to wrap the gift box? Explain. What is the surface area of the gift box? - Cubic units
A rectangular prism with a volume of 10 cubic units is filled with cubes with side lengths of 1/2 unit. How many 1/2 unit cubes does it take to fill the prism? - Chocolate - comparing
Robert has 8.2 cm, 3.1 cm, and 0.8 cm long chocolate. Norbert has 0.4 cm, 5 cm and 7.9 cm chocolate. Which one has more chocolate, and how much? - Calculate 73134
The wooden prism weighs 5 kg and has a 700 kg/m³ density. Calculate the volume of the wooden prism.
- Density 67774 The prism, whose base is square / the side of the square is 20 cm / 30 cm high, is made of oak wood and weighs 8.5 kg. What is the density of oak wood?
- Rectangular prism
What is the volume if I have a rectangular prism with a length of 1,000 cm, a width of 30 cm, and a height of 50 cm? - How high
How high does a prism with base dimensions of 1.7 dm and 5 dm reach if 1032 dm cubic will fit? - Garden
A Garden with an area of 800 square meters rained 3 mm of water. How many 10-liter cans of water are needed for the same irrigation? - Measuring 16183
The load capacity of the truck is 10t. Will it carry 200 oak planks measuring 30 cm, 4 m, and 30 mm at a time if the weight of 1 dm³ of oak wood is 0.7 kg?
Do you have unsolved problem that you need help? Ask a question, and we will try to solve it. Solving math problems.
See also more information on Wikipedia.
