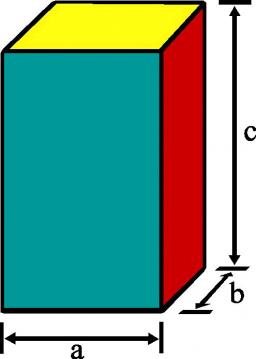
Rectangular prism
What is the volume if I have a rectangular prism with a length of 1,000 cm, a width of 30 cm, and a height of 50 cm?
Correct answer:
Tips for related online calculators
Tip: Our volume units converter will help you convert volume units.
You need to know the following knowledge to solve this word math problem:
Units of physical quantities:
Grade of the word problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Right rectangular prism
The right rectangular prism has a length of 3.2 feet, a width of 1.7 feet, and a height of 2.1 feet. What is its volume? 5.712 ft³ 7.54 ft³ 11.424 ft³ 31.46 ft³ - A rectangular 8
A rectangular prism has a length of 10m, a height of 9m, and a width of 15m. What is its volume in cubic meters? - Consumption 4259
What is the consumption of fabric per tent: Length 250, width 180, the height of triangle 120, sides 150 (all cm). What is the volume of air in the tent? - Beni has
Beni has a rectangular tub with a height of 50 cm, a width of 70 cm, and a length of 90 cm. He will fill the tub with water. The amount of water needed to fill 2/3 of Beni's tub is :
- Water overflow
A rectangular container has a length of 30 cm, a width of 20 cm, and a height of 24 cm. It is filled with water to a depth of 15 cm. Some water overflows when an additional 6.5 liters of water is poured into the container. How many liters of water overflo - Triangular prism
Calculate a triangular prism if it has a rectangular triangle base with a = 4cm and hypotenuse c = 50mm, and the height of the prism is 0.12 dm. - Precipitation 66874
The total precipitation for one day reached 22mm. How many hectoliters of water have rained on a rectangular garden measuring 32m and 45m?
