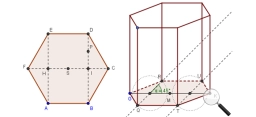
The volume 8
The volume of a right regular hexagonal prism is 187.2 cubic millimeters. The line segment that has a length of 2.6 millimeters begins at the center of the hexagon and ends at one side of the hexagon. 3 mm base. Find the height.
Correct answer:
Tips for related online calculators
Tip: Our volume units converter will help you convert volume units.
See also our trigonometric triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
- algebra
- expression of a variable from the formula
- solid geometry
- prism
- planimetrics
- polygon
- area of a shape
- triangle
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- Hexagonal prism
The prism's base is a regular hexagon consisting of six triangles with side a = 12 cm and height va = 10.4 cm. The prism height is 5 cm. Find the volume and surface of the prism. - Hexagonal pyramid
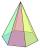Calculate the volume and the surface of a regular hexagonal pyramid with a base edge length of 3 cm and a height of 5 cm. - The regular
The regular triangular prism has a base in the shape of an isosceles triangle with a base of 86 mm and 6.4 cm arms, the height of the prism is 24 cm. Calculate its volume. - Hexagonal 66574
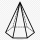The candle is made from wax in the shape of a regular hexagonal pyramid. It has a height of 6.5 cm and a length of the base edge of 3 cm. Find the volume of wax. - ABCDEFGHIJKL 8426
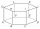The given is a regular hexagonal prism ABCDEFGHIJKL, which has all edges of the same length. Find the degree of the angle formed by the lines BK and CL in degrees. - Hexagon
Calculate the regular hexagonal prism's surface whose base edge a = 12cm and side edge b = 3 dm. - Coordinates hexagon
The regular hexagon ABCDEF is given. Point A has coordinates [1; 3], and point D has coordinates [4; 7]. Calculate the sum of the coordinates of the center of its described circle. - The rod
The rod has the shape of a regular hexagonal prism with a volume of 32.4 cubic decimetres. What is the area of the base if it is 350 centimeters long? Round to ones. - Triangular prism
The plane passing through the edge AB and the center of segment CC' of regular triangular prism ABCA'B'C' has an angle with base 22 degrees, |AB| = 6 cm. Calculate the volume of the prism. - Hexaprism container
Calculate the volume and surface in the shape of a regular hexagonal prism with a height of 1.4 m, a base edge of 3dm, and a corresponding height of 2.6 dm. - Four prisms
Question No. 1: The prism has the dimensions a = 2.5 cm, b = 100 mm, c = 12 cm. What is its volume? a) 3000 cm² b) 300 cm² c) 3000 cm³ d) 300 cm³ Question No.2: The prism base is a rhombus with a side length of 30 cm and a height of 27 cm. The height of t - Triangular prism The regular triangular prism has a base edge of 8.6 dm and a height of 1.5 m. Find its volume and surface area.
- Wooden prism
Find the weight of a regular wooden triangular prism with a height equal to the base's perimeter and a figure inscribed in a circle with a radius of 6.M cm, where M is the month of your birth. The density of oak is 680 kg/m³. - Hexagonal 6424
Calculate the volume and surface of a regular hexagonal prism, the base edge of which is 5 cm long and its height is 20 cm. - Hexagonal prism
Calculate the volume and surface of a regular hexagonal prism with the edge of the base a = 6 cm with the corresponding height v1 = 5.2cm and the height of the prism h = 1 dm. - Quarter-liter 3380
A container has the shape of a regular hexagonal prism with a base with a capacity of 0.5dm2, which three quarter-liter cups of water fill to the brim. What is the height of a container? - Hexagonal pyramid
Regular hexagonal pyramid has dimensions: length edge of the base a = 1.8 dm and the height of the pyramid = 2.4 dm. Calculate the surface area and volume of a pyramid.
