Practice problems of the space diagonal
Space diagonal (also interior diagonal or body diagonal) of a polyhedron (i.e. prism, cube or rectangular cuboid) is a line connecting two vertices that are not on the same face. Space diagonals contrast with face diagonals, which connect vertices on the same face (but not on the same edge) as each other.Number of problems found: 103
- Cube in ball
The cube is inscribed into the sphere of radius 181 dm. How many percent is the volume of cube of the volume of the sphere? - Sphere area
A cube with an edge 1 m long is a circumscribed sphere (vertices of the cube lie on a sphere's surface). Find the surface area of the sphere. - Cube into sphere
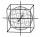The cube has brushed a sphere as large as possible. Determine how much percent the waste was. - Trunk
Calculate the length of the biggest fishing rod that can be inserted into the trunk of a car with dimensions 165 x 99 × 85 cm. - Volume and body diagonal
Calculate how much the volume and body diagonal of the cuboid decrease if we reduce each of its three edges, a, b, and c, by 18%. - Billiard balls
A layer of ivory billiard balls radius of 6.35 cm is in the form of a square. The balls are arranged so that each ball is tangent to everyone adjacent to it. In the spaces between sets of 4 adjacent balls, other balls rest, equal in size to the original. - Cubes
One cube is an inscribed sphere, and the other one is described. Calculate the difference of volumes of cubes if the difference of surfaces in 231 cm². - The glass
The glass has the shape of a cylinder with an inner diameter of 12 cm, and the height from the bottom is 16 cm. The cut skewer can be inserted diagonally into the glass so it does not protrude beyond the edge. What is the largest possible length of the cu - Cuboid diagonal
Calculate the volume and surface area of the cuboid ABCDEFGH, which sides a, b, and c has dimensions in the ratio of 9:3:8. If you know that the diagonal wall AC is 86 cm, and the angle between AC and space diagonal AG is 25 degrees. - Side wall planes
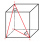Find the volume and surface of a cuboid whose side c is 30 cm long and the body diagonal forms angles of 24°20' and 45°30' with the planes of the side walls. - Faces diagonals
If a cuboid's diagonals are x, y, and z (wall diagonals or three faces), find the cuboid volume. Solve for x=1.3, y=1, z=1.2 - Four sided prism
Calculate the volume and surface area of a regular quadrangular prism whose height is 28.6cm, and the diagonal body forms a 50-degree angle with the base plane. - Distance of points
A regular quadrilateral pyramid ABCDV is given, in which edge AB = a = 4 cm and height v = 8 cm. Let S be the center of the CV. Find the distance of points A and S. - Right triangular prism
We have a cuboid with a base and dimensions of 12 cm and 5 cm and a height of 4 cm. The tablecloth is cut into two identical triangular prisms with right triangular bases. We painted the surface of the created prisms with color. Calculate the surface area - Quadrilateral prism
The height of a regular quadrilateral prism is v = 10 cm, and the deviation of the body diagonal from the base is 60°. Determine the length of the base edges, the surface, and the prism's volume. - Quadrilateral prism
Calculate the volume (V) and the surface (S) of a regular quadrilateral prism whose height is 28.6 cm and the deviation of the body diagonal from the base plane is 50°. - Deviation of the lines
Find the deviation of the lines AG, BH in the ABCDEFGH box-cuboid, if given | AB | = 3cm, | AD | = 2cm, | AE | = 4cm - Forces
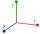In point, O acts three orthogonal forces: F1 = 20 N, F2 = 7 N, and F3 = 19 N. Determine the resultant of F and the angles between F and forces F1, F2, and F3. - Space diagonal angles
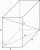Calculate the angle between the body diagonal and the side edge c of the block with dimensions: a = 28cm, b = 45cm, and c = 73cm. Then, find the angle between the body diagonal and the plane of the base ABCD. - Cuboid face diagonals
The lengths of the cuboid edges are in the ratio 1: 2: 3. Will the lengths of its diagonals be in the same ratio? The cuboid has dimensions of 5 cm, 10 cm, and 15 cm. Calculate the size of the wall diagonals of this cuboid.
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
