Tělesová úhlopříčka - příklady
Tělesná úhlopříčka (také vnitřní úhlopříčka nebo prostorová úhlopříčka) mnohostěnu (tj. hranolu, kostky nebo pravoúhlého kvádru) je čára spojující dva vrcholy, které nejsou na téže stěně. Prostorové úhlopříčky kontrastují se stěnovými úhlopříčkami, které navzájem spojují vrcholy na stejné stěně (ale ne na stejné hraně).Pokyny: Každý problém vyřešte pečlivě a pro každý úkol uveďte podrobné řešení.
Počet nalezených příkladů: 117
- Krychle
Krychli o hraně 1 m je opsána koule (vrcholy krychle leží na povrchu koule). Určete velikost povrchu teto koule. - Objem a tělesová úhlopříčka
Vypočítejte, o kolik procent se zmenší objem a tělesová úhlopříčka kvádru, jestliže každou z jeho tří hran a, b, c zmenšíme o 18%? - Kostka v kouli
Kostka je vepsána do koule o poloměru 6 dm. Kolik procent tvoří objem kostky z objemu koule? - Krychle 41
Krychle o hraně a je zbroušena na kouli o co největším objemu. Urči, kolik % činil odpad z broušení. - Krychle
Jedna krychle je kouli vepsána a druhá opsána. Vypočítejte rozdíl objemů v obou krychlích, pokud rozdíl jejich povrchů je 231 dm². - Dvě koule
Dvě koule, jedna s poloměrem 8 cm a další s poloměrem 6 cm, se vloži do válcové plastové nádoby s poloměrem 10 cm. Najděte množství vody potřebné k jejich potopení. - Petra 4
Petra má ve dvou bedničkách tvaru krychle zasazené květiny. První bednička má vnitřní rozměr 70 cm a druhá 5dm. Chce si vyrobit jednu bedničku tvaru kvádru, kam by obě květiny z těchto bedniček přesadila. Nová bednička má mít stejný vnitřní objem jako obě - Kvádr težší Kvádr má objem 32 cm³. Jeho plášť má dvojnásobný obsah než jedna ze čtvercových podstav. Jakou délku má tělesová úhlopříčka?
- Kvádr
Kvádr s hranou a=7 cm a tělesových úhlopříčkou u=33 cm má objem V=3136 cm³. Vypočítejte velikosti ostatních hran. - Kvádr 68
Kvádr má tělesovou úhlopříčku u=25 cm a strana b je oproti straně a o třetinu delší. Jaký je objem kvádru? - Kulečník
Vrstva slonovinových kulečníkových koulí o poloměru 6,35 cm, je ve tvaru čtverce. Koule jsou uspořádány tak, že každá koule je tangenty (dotýká se) každé sousedící s ní. V prostorech mezi 4 přilehlými koulemi je prostor rovný velikosti originálu kouli. Po - Drátěný model
Drátěný model pravidelného šestibokého hranolu s podstavnou hranou délky a = 8 cm má výšku v = 12 cm. Těleso se přelepí papírem, podstavy tmavým a plášť bílým. - Vypočtěte v cm největší možnou přímou vzdálenost dvou vrcholů drátěného hranolu (tloušťku drá - Krychle
Krychle je vepsána do koule o objemu 1579 cm³. Určete délku hrany krychle. - Součet velikostí hran
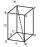Vypočtěte povrch kvádru, je-li dán součet velikostí jeho hran a+b+c=19 cm a velikost tělesové úhlopříčky u=13 cm. - Síly
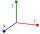Na bod T působí tři navzájem kolmé síly F1 = 18 N, F2 = 16 N, F3 = 4 N. Určete výslednici F a úhly, které svírá výslednice se složkami F1, F2, F3. - Odchylka úhlopříčky
Objem kvádru se čtvercovou podstavou je 64 cm³ a odchylka tělesové úhlopříčky od roviny podstavy je 45 stupňů. Vypočítejte jeho povrch. - Vypočítej 80
Vypočítej, vejde-li se obdélníkový obraz s rozměry 33cm a 70cm do kufru s rozměry 65cm, 40cm a 20cm. Udělej si náčrtek, zapiš jako slovní úlohu. - Kvádr
Vypočtěte objem a povrch kvádru ABCDEFGH, jehož rozměry abc jsou v poměru 4:10:4, víte-li ze stenova úhlopříčka AC měří 46 cm a má od telesové úhlopříčky AG odchylku 55 stupňů. - Objem
Objem pravidelného čtyřbokého hranolu je 192 cm³. Velikost jeho podstavné hrany a tělesových výšky jsou v poměru 1:3. Vypočítejte povrch hranolu. - Maximální délka tyče v kontejneru
Do přepravního kontejneru o rozměrech a=10 m, b=4m, c=3m byla umístěna dřevěná bedna o rozměrech d=3m, e=4m a f=3m. Jaká je maximální délka rovné neohebné tyče se zanedbatelným průměrem, kterou lze v této situaci ještě do kontejneru umístit?
Máš příklad z matematiky, který jsi tady nenašel vyřešený? Pošli nám příklad a my Ti ho zkusíme vypočítat.
