Telesová uhlopriečka - príklady
Telesová uhlopriečka (tiež vnútorná uhlopriečka alebo priestorová uhlopriečka) mnohostenu (t. j. hranolu, kocky alebo pravouhlého kvádra) je čiara spájajúca dva vrcholy, ktoré nie sú na tej istej stene. Priestorové uhlopriečky kontrastujú s stenovými uhlopriečkami, ktoré navzájom spájajú vrcholy na rovnakej stene (ale nie na rovnakej hrane).Pokyny: Vyriešte každú úlohu starostlivo a ukážte svoje celé riešenie. Ak je to vhodné, vykonajte skúšku správnosti riešenia.
Počet nájdených príkladov: 118
- Kocka v guľi
Kocka je vpísaná do gule s polomerom 324 cm. Koľko percent tvorí objem kocky z objemu gule? - Kocka
Kocke s hranou 1 m je opísaná guľa (vrcholy kocky ležia na povrchu gule). Určte veľkosť povrchu teto gule. - Objem a telesová uhlopriečka
Vypočítaj, o koľko percent sa zmenší objem a telesová uhlopriečka kvádra, ak každú z jeho troch hrán a, b,c zmenšíme o 18%? - Kocka na guľu
Kocka o hrane a je zbrúsené na guľu o čo najväčšom objeme. Urči, koľko % predstavoval odpad z brúsenia.
- Kváder 36
Dĺžky hrán kvádra sú v pomere 2:3:6. Jeho telesová uhlopriečka má dĺžku 14 cm. Vypočítajte objem a povrch kvádra. - Debničky
Petra má v dvoch debničkách tvaru kocky zasadené kvety. Prvá debnička má vnútorný rozmer 70 cm a druhá 5dm. Chce si vyrobiť jednu debničku tvaru kvádra, kam by obidve kvety z týchto debničiek presadila. Nová debnička má mať rovnaký vnútorný objem ako obe - Kváder
Kváder s hranou a=25 cm a telesovou uhlopriečkou u=57 cm má objem V=32000 cm³. Vypočítajte veľkosti ostatných hrán. - Kváder s podstavou
Kváder s podstavou a rozmermi 12 cm a 5 cm a výškou 4 cm. Stolár tento kváder rozrezal na dva zhodné trojboké hranoly s podstavami v tvare pravouhlého trojuholníka. Stolár vytvorené hranoly natrel farbou. Vypočítajte povrch jedného z týchto dvoch trojboký - Biliardové gule
Vrstva slonovinových biliardových gúľ o polomere 6,35 cm, je v tvare štvorca. Gule sú usporiadané tak, že každá guľa je tangenta (dotýka sa) každej susediacej s ňou. V priestoroch medzi 4 priľahlými guľami je priestor rovný veľkosti originálej guli. Po se
- Uhlopriečku 77724
Kváder má telesovú uhlopriečku u=25 cm a strana b je oproti strane a o tretinu dlhšia. Aký je objem kvádra? - Guľa a kúžel
Do gule s polomerom G = 41 cm vpíšte kužel s najväčším objemom. Aký je tento objem a aké sú rozmery kužela? - Pravidelného 11111
Drôtený model pravidelného šesťbokového hranola s podstavnou hranou dĺžky a = 8 cm má výšku v = 12 cm. Teleso sa prelepí papierom, podstavy tmavým a plášť bielym. - Vypočítajte v cm najväčšiu možnú priamu vzdialenosť dvoch vrcholov drôteného hranola (hrúb - Objem 40
Objem kvádra so štvorcovou podstavovou je 64 cm³ a odchýlka telesovej uhlopriečky od roviny podstavy je 45 stupňov. Vypočítajte jeho povrch. - Kváder
Vypočítajte objem a povrch kvádra ABCDEFGH, ktorého rozmery abc sú v pomere 9:4:8, ak viete že stenová uhlopriečka AC meria 95 cm a má od telesovej uhlopriečky AG má odchýlku 30 stupňov.
- Guľa vs. kocka
Koľko % povrchu gule s polomerom 12 cm tvorí povrch kocky vpísanej robiť teto gule? - Mimobežky
Je daný kváder ABCDEFGH. Vieme, že |AB| = 1 cm, |BC| = 2 cm, |AE| = 3 cm. Vypočítajte v stupňoch veľkosť uhla, ktorý zvierajú priamky BG a FH . - Sily
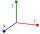Na bod I pôsobia tri navzájom kolmé sily F1=6 N, F2=15 N, F3=20 N. Určte výslednicu F a uhly, ktoré zviera výslednica so zložkami F1, F2, F3. - Matematika 2
Do prepravného kontajnera s rozmermi a=10 m, b=4m, c=3m bola umiestnená drevená debna s rozmermi d=3m, e=4m a f=3m. Aká je maximálna dĺžka rovnej neohybnej tyče so zanedbateľným priemerom, ktorú je možné v tejto situácii ešte do kontejnera umiestniť? - Výška 18
Výška pravidelného štvorbokého hranola je v=10 cm, odchýlka telesovej uhlopriečky od podstavy je 60°. Určte dĺžku podstavových hrán, povrch a objem kvádra.
Pohár má tvar valca s vnútorným priemerom 12 cm, výška pohára od dna je 16 cm. Zrezanú špajdľu je možné šikmo vložiť do pohára tak, že neprečnieva cez okraj. Aká je najväčšia možná dĺžka zrezanej špajdle? (Hrúbka špajdle sa pri výpočte zanedbáva.)Máš úlohu, nad ktorou si lámeš aspoň 10 minút hlavu? Pošli nám úlohu a my Ti ju skúsime vypočítať. Riešenie príkladov z matematiky.
