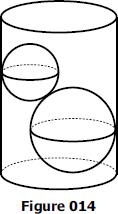
Dvě koule
Dvě koule, jedna s poloměrem 8 cm a další s poloměrem 6 cm, se vloži do válcové plastové nádoby s poloměrem 10 cm. Najděte množství vody potřebné k jejich potopení.
Vaše odpověď:
Vaše odpověď:
Zobrazuji 4 komentáře:
Žák
nechápu jak jste se dopracovali ke V=............................. předposlední řádek výpočtu
Www
no napr. x je vodorovna vzdalenost stredov gul. Je to logicke ak od priemeru valca (20 cm) odcitame po bokoch r a R. h je zvisla vzdalenost stredov gul. To je cista Pytagovoa veta. H je celkova vyska "vody" vo valci. Objemy su snad trivialne.... vzorec dosadis a mas...
Tipy na související online kalkulačky
Tip: Převody jednotky objemu vám pomůže naše kalkulačka pro převody jednotek objemu.
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
aritmetikastereometrieplanimetrieJednotky fyzikálních veličinÚroveň náročnosti úkolu
Doporučujeme k tomuto príkladu si prohlédnout toto výukové video: video1
Související a podobné příklady:
- Kuličky 11
Do válcové nádoby s vodou, stojící na vodorovném povrchu, bylo vhozeno 20 stejných ocelových kuliček tak, že byly všechny ponořené pod hladinou. Hladina vody se přitom zvedla o 4 mm. Urči poloměr jedné kuličky, jestliže průměr válcové nádoby je 4,7 cm. - Když bylo
Když bylo do válcové nádoby naplněné vodou ponořeno těleso, hladina vody v nádobě stoupla o 28 mm. Vypočítejte objem ponořeného tělesa, víte-li, že průměr dna nádoby je 8 cm. - Průměr válcové nádoby
Jaký je průměr nádoby tvaru válce, pokud v ní půl litru vody sahá do výšky 12 cm? - Voda
Do plné válcové nádrže vysoké 2,9 m s poloměrem podstavy 2,7 m vložíme těleso tvaru kvádru o rozměrech 1,5 m, 1,2 m, 1,5 m. Kolik litrů vody vyteče? - Kolik 123
Kolik litrů se vejde do válcové nádoby s obsahem podstavy 0,06 m(2) a výškou 5 cm? - Valcová nádoba
Do válcové nádoby vlily 3,5 litru vody. Pokud měla nádoba průměr podstavy 3 dm, voda sahala přibližně do jaké výšky? - Válcová 4
Válcová nádoba s průměrem dna 30 cm a výškou 20 cm je plná vody. Vodu chceme přelít do jiné válcové nádoby s průměrem dna 15 cm. Jakou minimální výšku musí mít druhá nádoba, aby se do ní voda vešla?
