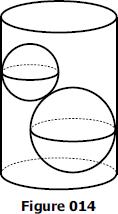
Two balls

Two balls, one 8cm in radius and the other 6cm in radius, are placed in a cylindrical plastic container 10cm in radius. Find the volume of water necessary to cover them.

Correct answer:

V =  5322.6258 cm3

Step-by-step explanation:

r=8 R=6 x=2⋅ 10−r−R=2⋅ 10−8−6=6 h=(r+R)2−x2=(8+6)2−62=4 10≐12.6491 H=h+r+R=12.6491+8+6≐26.6491 V1=π⋅ 102⋅ H=3.1416⋅ 102⋅ 26.6491≐8372.065 V2=4/3π⋅ r3=4/3⋅ 3.1416⋅ 83≐2144.6606 V3=4/3π⋅ R3=4/3⋅ 3.1416⋅ 63≐904.7787 V=V1−V2−V3=8372.065−2144.6606−904.7787=5322.6258 cm3

Try another example


We will be pleased if You send us any improvements to this math problem. Thank you!






avatar




Tips to related online calculators
Tip: Our volume units converter will help you with the conversion of volume units.
Pythagorean theorem is the base for the right triangle calculator.
See also our trigonometric triangle calculator.

You need to know the following knowledge to solve this word math problem:


 
We encourage you to watch this tutorial video on this math problem: video1   video2   video3

Related math problems and questions:

  • Metal balls
    three_circles_inside_one Four metal balls with a diameter of 5 cm are placed in a measuring cylinder with an inner diameter of 10 cm. What is the smallest water volume to be poured into the cylinder so that all balls are below the water level?
  • Cube in sphere
    sphere4 The sphere is an inscribed cube with an edge of 8 cm. Find the sphere's radius.
  • Body diagonal
    kvadr_diagonal Calculate the volume of a cuboid whose body diagonal u is equal to 6.1 cm. Rectangular base has dimensions of 3.2 cm and 2.4 cm
  • Body diagonal
    cubes3 Find the cube surface if its body diagonal has a size of 6 cm.
  • Cuboid
    cuboid Cuboid ABCDEFGH with 10 cm height has a base edge length 6 cm and 8 cm. Determine angle between body diagonal and the base plane (round to degrees).
  • The cylindrical container
    balls2 The cylindrical container has a base area of 300 cm3 and a height of 10 cm. It is 90% filled with water. We gradually insert metal balls into the water, each with a volume of 20 cm3. After inserting how many balls for the first time does water flow over
  • Tangent spheres
    tangent_spheres A sphere with a radius of 1 m is placed in the corner of the room. What is the largest sphere size that fits into the corner behind it? Additional info: Two spheres are placed in a corner of a room. The spheres are each tangent to the walls and floor and
  • Body diagonal
    diagonal Calculate the length of the body diagonal of the 6cm cube.
  • The cone - S,V
    kuzel Calculate the volume and surface area of the cone if its radius r = 6 cm and side s = 10 cm.
  • Body diagonal
    cuboid Find the length of the body diagonal of a cuboid with lengths of 16 cm, 7 cm, and 4 cm.
  • Body diagonal
    space_diagonal Calculate the length of the body diagonal of a block with dimensions: a = 20 cm, b = 30 cm, c = 15 cm.
  • Body diagonal - cube
    cube_shield Calculate the surface and cube volume with body diagonal 15 cm long.
  • Plasticine ball
    p_balls Plasticine balls have radius r1=85 cm, r2=60 mm, r3=59 cm, r4=86 cm, r5=20 cm, r6=76 mm, r7=81 mm, r8=25 mm, r9=19 mm, r10=14 cm. For these balls
  • Cube diagonals
    krychlicka Determine the volume and surface area of the cube if you know the length of the body diagonal u = 216 cm.
  • Body diagonal
    kvadr Cuboid with base 7cm x 3,9cm and body diagonal 9cm long. Find the height of the cuboid and the length of the diagonal of the base,
  • Space diagonal angles
    kvadr_diagonal Calculate the angle between the body diagonal and the side edge c of the block with dimensions: a = 28cm, b = 45cm and c = 73cm. Then, find the angle between the body diagonal and the plane of the base ABCD.
  • Angle of diagonal
    hranol The angle between the body diagonal of a regular quadrilateral and its base is 60°. The edge of the base has a length of 10cm. Calculate the body volume.