Distance of points
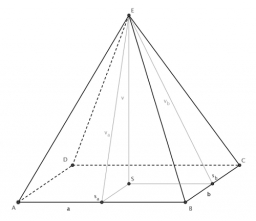
A regular quadrilateral pyramid ABCDV is given, in which edge AB = a = 4 cm and height v = 8 cm. Let S be the center of the CV. Find the distance of points A and S.
Your answer:
Your answer:
Tips for related online calculators
See also our right triangle calculator.
Cosine rule uses trigonometric SAS triangle calculator.
See also our trigonometric triangle calculator.
Cosine rule uses trigonometric SAS triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
geometryalgebrasolid geometryplanimetrygoniometry and trigonometryUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- Pyramid volume surface
Find the volume and surface area of a regular quadrilateral pyramid ABCDV if its leading edge has a length a = 10 cm and a body height h = 12 cm. - Angle of two lines
There is a regular quadrilateral pyramid ABCDV; | AB | = 4 cm; height v = 6 cm. Determine the angles of lines AD and BV. - Pyramid - angles In a regular pyramid in which the edge of the base is | AB | = 4 cm; height = 6 cm, calculate the angle of the lines AV and CV, V = vertex.
- Height of pyramid
The pyramid ABCDV has edge lengths: AB = 4, AV = 7. What is its height? - Special body
Above each wall of a cube with an edge a = 30 cm, we construct a regular quadrilateral pyramid with a height of 15 cm. Find the volume of the resulting body. - Pyramid intersection
Given a regular quadrilateral pyramid ABCDV, point M is inside its edge AV, and point N is on the long line DC beyond point C. Construct the intersection of the plane MNV with the plane BCV and the intersection of the line MN and the plane BCV. - Quadrilateral pyramid
Find the height and surface of a regular quadrilateral pyramid with a base edge a = 8 cm and a wall height w = 10 cm. Sketch a picture.
