Vzdálenost bodů
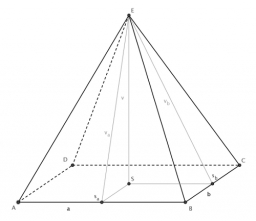
Je dán pravidelný čtyřboký jehlan ABCDV, ve kterém AB = a = 4 cm a v = 8 cm. Nechť S je střed CV. Vypočítejte vzdálenost bodů A a S.
Správná odpověď:
Tipy na související online kalkulačky
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Kosinovú větu přímo používá kalkulačka SUS trojúhelníku.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Kosinovú větu přímo používá kalkulačka SUS trojúhelníku.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
geometriealgebrastereometrieplanimetriegoniometrie a trigonometrieJednotky fyzikálních veličinÚroveň náročnosti úkolu
Doporučujeme k tomuto príkladu si prohlédnout toto výukové video: video1
Související a podobné příklady:
- Průsečík přímky a roviny
 Je dán pravidelný čtyřboký jehlan ABCDV, uvnitř jeho hrany AV je bod M, na prosloužené úsečce DC za bod C je bod N. Sestrojte průsečnici roviny MNV s rovinou BCV a průsečík přímky MN a roviny BCV.
Je dán pravidelný čtyřboký jehlan ABCDV, uvnitř jeho hrany AV je bod M, na prosloužené úsečce DC za bod C je bod N. Sestrojte průsečnici roviny MNV s rovinou BCV a průsečík přímky MN a roviny BCV. - Tětiva 16
 Je dána kružnice k(S, r=6cm) a na ní body A, B tak, že /AB/ = 8cm. Vypočítej vzdálenost středu S kružnice k od středu C úsečky AB.
Je dána kružnice k(S, r=6cm) a na ní body A, B tak, že /AB/ = 8cm. Vypočítej vzdálenost středu S kružnice k od středu C úsečky AB. - Čtyřboký jehlan
 Je dán pravidelný čtyřboký jehlan ABCDV; | AB | = 4cm; v = 6cm. Určete úhel přímek AD a BV.
Je dán pravidelný čtyřboký jehlan ABCDV; | AB | = 4cm; v = 6cm. Určete úhel přímek AD a BV. - Je dán 13
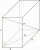 Je dán pravidelný čtyřboký hranol ABCDEFGH s podstavnou hranou AB délky 8 cm a výškou 6 cm. Bod M je střed hrany AE. Určete vzdálenost bodu M od roviny BDH.
Je dán pravidelný čtyřboký hranol ABCDEFGH s podstavnou hranou AB délky 8 cm a výškou 6 cm. Bod M je střed hrany AE. Určete vzdálenost bodu M od roviny BDH. - Hrana podstavy
 V pravidelném jehlanu, ve kterém hrana podstavy je |AB|=4cm; výška = 6cm vypočítej úhel přímek AV a CV, V = vrchol.
V pravidelném jehlanu, ve kterém hrana podstavy je |AB|=4cm; výška = 6cm vypočítej úhel přímek AV a CV, V = vrchol. - Čtyřboký jehlan 4
 Je dán pravidelný čtyřboký jehlan s délkou podstavné hrany a = 3 cm a s délkou boční hrany h = 8 cm. Vypočítejte prosím jeho povrch a objem.
Je dán pravidelný čtyřboký jehlan s délkou podstavné hrany a = 3 cm a s délkou boční hrany h = 8 cm. Vypočítejte prosím jeho povrch a objem. - Čtyřboký jehlan 9
 Je dán pravidelný čtyřboký jehlan. Délka hrany podstavy a = 6,5 cm, boční hrana s = 7,5 cm. Vypočítejte objem a obsah pláště.
Je dán pravidelný čtyřboký jehlan. Délka hrany podstavy a = 6,5 cm, boční hrana s = 7,5 cm. Vypočítejte objem a obsah pláště.
