Kosinus - příklady
Počet nalezených příkladů: 286
- Tunel - čtyřúhelník
Jak dlouhý bude tunel AB, vzdálenosti AD=35 m, DC=120 m, CB=85 ma úhly ADC=105 stupňů a BCD=71 stupňů. ABCD je čtyřúhelník. - Na hmotný
Na hmotný bod M působí síly F1, F2 o velikosti 40N. Jejich výslednice má velikost 60N. Určete úhel, který síly F1 a F2 svírají. - Nepravidelný čtyřúhelník
Vypočítej velikost strany d = |AD| ve čtyřúhelníku ABCD: a= 35m, b= 120m, c=85m, úhel ABC = 105 stupňů, úhel BCD= 72 stupňů - Souřadnicova soustava
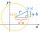V kartézské souřadnicové soustavě je dána jednotková kružnice, na které leží body A a B. Bod O je počátek a má souřadnice (0,0) a bod B souřadnice (1,0). Velikost úhlu BOA je 151°. Určete x-ovou souřadnici bodu A. - Rovnoramenný - osy uhlov
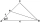V rovnoramenném trojúhelníku ABC se základnou AB platí ∠BAC = 20°, AB = 4. Osa vnitřního úhlu u vrcholu B protíná stranu AC v bodě P. Vypočítejte délku úsečky AP. Výsledek uveďte s přesností na dvě desetinná místa. - Odvěsna a úhly
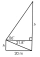V pravoúhlém trojúhelníku DEF s přeponou f = 12 cm má vnitřní úhel při vrcholu D velikost 60°. Jaká je délka odvěsny e? - Trojúhelníku 84015
V pravoúhlém trojúhelníku ABC přepona c = 8 cm a odvěsna b = 4 cm. Jaká je velikost úhlu α?
- Vypočítej 433
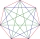Vypočítej obvod pravidelného sedmiúhelníku, je-li dána délka jeho nejkratší úhlopříčky u=14,5cm. - Střecha 18
Střecha našeho domu má tvar obdélníku. Při dešti se voda ze střechy svádí okapem. Kolik vody z naší střechy steklo při bouřce, když když víme, že na každý 1 m² plochy spadlo 12 l vody? střecha šířka 6m délka 9m a sklon roviny strechy je 37°. - Trojuhelníku 135
Trojuhelníku ABC o stranách a = 15 cm, b = 17,4 cm, c = 21,6 cm je opsána kružnice. Vypočítejte obsah úsečí určených stranami trojúhelníku. - Vzdálenost 145
Vzdálenost tětivy od středu je 6 cm. Středový úhel je 60°. Vypočítejte plošný obsah kruhové úseče. - Rovnoramenném 83247
Vypočítejte délky stran v rovnoramenném trojúhelníku, je-li dána výška (na základnu) Vc= 8,8cm a úhel u základny alfa= 38°40`. - Užitím 2
Užitím kosinové věty dokažte, že v rovnoramenném trojúhelníku ABC se základnou AB platí, že c=2a cos α. - V trojúhelníku 8
V trojúhelníku ABC znáte poměr délek stran a:b:c=3:4:6. Vypočítejte velikosti úhlů trojúhelníku ABC. - Vypočítejte kvádr
Je dán kvádr ABCDEFGH. Víme, že |AB| = 1 cm, |BC| = 2 cm, |AE| = 3 cm. Vypočítejte ve stupních velikost úhlu, který svírají přímky BG a FH .
- Nepřístupných 82710
Určete vzdálenost dvou nepřístupných míst K, L, pokud se z bodů A, B, které jsou od sebe vzdáleny 870 m, naměřily velikosti úhlů KAL=62°10", LAB=41°23", KBL=66°34", LBA = 34°52". Děkuji. - Trojúhelníku 82696
V trojúhelníku ABC je dáno b=5 cm, c=6 cm, /BAC/ = 80°. Vypočítejte velikosti ostatních stran a úhlů, dále určete velikosti těžnice tc a obsah trojúhelníku. - Vypočítejte 82695
Dán je rovnoběžník KLMN, ve kterém známe velikosti stran/KL/ = a = 84,5 cm, /KN/ = 47,8 cm a velikost úhlu při vrcholu K 56°40´. Vypočítejte velikost úhlopříček. - Trojúhelníku 82578 Vrcholy trojúhelníku ABC jsou: A[1, 2, -3], B[0, 1, 2], C[2, 1, 1]. Vypočítejte délky stran AB, AC a úhel při vrcholu A.
- Spádnice
Určit objem a povrch kužele, jehož spádnice o délce 8cm svírá s rovinou podstavy úhel 75 stupňů
Máš příklad, nad kterým si přemýšlíš alespoň 10 minut? Pošli nám příklad a my Ti ho zkusíme vypočítat.
