Cosine - practice problems
The cosine function is a trigonometric ratio representing the relationship between an angle and the ratio of the adjacent side to the hypotenuse in a right triangle. Written as cos(θ), it ranges from -1 to 1 and is closely related to the sine function through the identity sin²(θ) + cos²(θ) = 1. The cosine graph is a wave similar to sine but shifted by 90 degrees (π/2 radians). Cosine appears in the law of cosines for general triangles, Fourier analysis, and physics formulas involving work and projection. It models periodic phenomena and is essential for vector operations, particularly in calculating dot products. The function is even, meaning cos(-θ) = cos(θ).Number of problems found: 294
- Three angles
 Find all missing values of angles using the Law of Cosines if given all sides: a=12, b=13, and c=20
Find all missing values of angles using the Law of Cosines if given all sides: a=12, b=13, and c=20 - ABCD rhombus
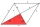 ABCD is a rhombus with sides 10.5cm. If the length of the diagonal AC=15.8cm, using cosine formula. a. calculate the length of the diagonal BD correct to the nearest cm b. the angles of the rhombus to the nearest degree.
ABCD is a rhombus with sides 10.5cm. If the length of the diagonal AC=15.8cm, using cosine formula. a. calculate the length of the diagonal BD correct to the nearest cm b. the angles of the rhombus to the nearest degree. - Vertical components
 Find the horizontal and vertical components of the vector which has magnitude 750 as shown in the following figure.
Find the horizontal and vertical components of the vector which has magnitude 750 as shown in the following figure. - Triangle 90
 Triangle made by 6 cm 4.5 cm and 7.5 cm. what angles does it make?
Triangle made by 6 cm 4.5 cm and 7.5 cm. what angles does it make? - Rhombus 36
 Rhombus ABCD with side 8 cm long has diagonal BD 11.3 cm long. Find angle DAB.
Rhombus ABCD with side 8 cm long has diagonal BD 11.3 cm long. Find angle DAB. - X-triangle
 Find the length of the x segment in the given triangle drawings.
Find the length of the x segment in the given triangle drawings. - Trigonometric fx
 When an acute angle φ is in the standard position, its terminal side passes through point P (1,3). Find trigonometric functions of angle θ : sin φ, cos φ, tan φ, cotan φ.
When an acute angle φ is in the standard position, its terminal side passes through point P (1,3). Find trigonometric functions of angle θ : sin φ, cos φ, tan φ, cotan φ. - Cosine - legs
 Using the law of cosines, find the measurement of leg b if the givens are β=20°, a=10, and c=15.
Using the law of cosines, find the measurement of leg b if the givens are β=20°, a=10, and c=15. - Three 235
 Three houses form a triangular shape. House A is 50 feet from house C and house B is 60 feet from house C. The measure is angle ABC is 45 degrees. Draw a picture and find the distance between A and B.
Three houses form a triangular shape. House A is 50 feet from house C and house B is 60 feet from house C. The measure is angle ABC is 45 degrees. Draw a picture and find the distance between A and B. - Piece of a wire
 A piece of wire is bent into the shape of a triangle. Two sides have lengths of 24 inches and 21 inches. The angle between these two sides is 55°. What is the length of the third side to the nearest hundredth of an inch? A: The length of the third side is
A piece of wire is bent into the shape of a triangle. Two sides have lengths of 24 inches and 21 inches. The angle between these two sides is 55°. What is the length of the third side to the nearest hundredth of an inch? A: The length of the third side is - A right
 A right triangle has side lengths a=3, b=5, and c=4, as shown below. Use these lengths to find tan x, sin x, and cos x.
A right triangle has side lengths a=3, b=5, and c=4, as shown below. Use these lengths to find tan x, sin x, and cos x. - Subtract polar forms
 Solve the following 5.2∠58° - 1.6∠-40° and give answer in polar form
Solve the following 5.2∠58° - 1.6∠-40° and give answer in polar form - Conjugate coordinates
 If the rectangular conjugate of the polar vector 12 angle 35 degrees is equal to x+yi, find the sum of x and y.
If the rectangular conjugate of the polar vector 12 angle 35 degrees is equal to x+yi, find the sum of x and y. - Cplx sixth power
 Let z = 2 - sqrt(3i). Find z6 and express your answer in rectangular form. if z = 2 - 2sqrt(3 i) then r = |z| = sqrt(2 ^ 2 + (- 2sqrt(3)) ^ 2) = sqrt(16) = 4 and theta = tan -2√3/2=-π/3
Let z = 2 - sqrt(3i). Find z6 and express your answer in rectangular form. if z = 2 - 2sqrt(3 i) then r = |z| = sqrt(2 ^ 2 + (- 2sqrt(3)) ^ 2) = sqrt(16) = 4 and theta = tan -2√3/2=-π/3 - A triangle 7
 A triangle lot has the dimensions a=15m, b=10m, and c=20m. What is the measure of the angle between the sides of b and c?
A triangle lot has the dimensions a=15m, b=10m, and c=20m. What is the measure of the angle between the sides of b and c? - Tunnel - quadrilateral
 How long will the tunnel AB be, distances AD=35 m, DC=120 m, CB=85 m, and angles ADC=105 degrees and BCD=71 degrees. ABCD is a quadrilateral.
How long will the tunnel AB be, distances AD=35 m, DC=120 m, CB=85 m, and angles ADC=105 degrees and BCD=71 degrees. ABCD is a quadrilateral. - On a mass
 The forces F1, and F2 with magnitudes of 40N act on a mass point M. Their resultant has a magnitude of 60N. Determine the angle that the forces F1 and F2 make.
The forces F1, and F2 with magnitudes of 40N act on a mass point M. Their resultant has a magnitude of 60N. Determine the angle that the forces F1 and F2 make. - Quadrilateral - irregular
 Find the length of the side d = |AD| in quadrilateral ABCD: a= 35m, b= 120m, c=85m, angle ABC = 105 degrees, angle BCD= 72 degrees
Find the length of the side d = |AD| in quadrilateral ABCD: a= 35m, b= 120m, c=85m, angle ABC = 105 degrees, angle BCD= 72 degrees - Unit circle
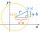 In the Cartesian coordinate system, a unit circle is given on which points A and B lie. Point O is the origin and has coordinates (0,0) and point B has coordinates (1,0). The size of angle BOA is 151°. Determine the x-coordinate of point A.
In the Cartesian coordinate system, a unit circle is given on which points A and B lie. Point O is the origin and has coordinates (0,0) and point B has coordinates (1,0). The size of angle BOA is 151°. Determine the x-coordinate of point A. - Maturitný - RR - base
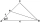 In an isosceles triangle ABC with base AB, ∠BAC = 20°, AB = 4. The axis of the interior angle at vertex B intersects side AC at point P. Calculate the length of the segment AP. Give the result to two decimal places.
In an isosceles triangle ABC with base AB, ∠BAC = 20°, AB = 4. The axis of the interior angle at vertex B intersects side AC at point P. Calculate the length of the segment AP. Give the result to two decimal places.
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
