Tětiva 16
Je dána kružnice k(S, r=6 cm) a na ní body A, B tak, že /AB/ = 8 cm. Vypočítej vzdálenost středu S kružnice k od středu C úsečky AB.
Vaše odpověď:
Vaše odpověď:
Tipy na související online kalkulačky
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
algebraplanimetrieÚroveň náročnosti úkolu
Doporučujeme k tomuto príkladu si prohlédnout toto výukové video: video1
Související a podobné příklady:
- Tětiva
Na kružnici k(S;r=8 cm) jsou různé body A, B spojené úsečkou /AB/=12 cm. Střed AB označ S´. Vypočítej /SS´/. Proveď náčrtek. - Sečna kružnice
Daná je kružnice k(S,4 cm) a přímka p. Je-li vzdálenost bodu S od přímky p je menší než 4 cm, pak přímka p se nazývá? - Kružnice a body
Daná je kružnice k(S; 8 cm). Dále jsou dány body K, L tak, že platí: délka SL je 6 cm, délka SM je větší než 8 cm. Které z následujících tvrzení není pravdivé a. Kružnice m(M; |ML|) má s kružnicí ke společnému právě dva body. b. Kružnice p(L; |LS|) má s k - Z7-1-6 MO 2018
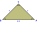Je dán rovnoramenný pravoúhlý trojúhelník ABS se základnou AB. Na kružnici, která má střed v bodě S a prochází body A a B, leží bod C tak, že trojúhelník ABC je rovnoramenný. Určete, kolik bodů C vyhovuje uvedeným podmínkám, a všechny takové body sestrojt - Poloměr 10
Poloměr kružnice r=8,9 cm, tětiva AB této kružnice má délku 16 cm. Vypočítej vzdálenost tětivy AB od středu kružnice . - Úhel v čtyřúhelníku
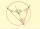Body ABC leží na kružnici k(S, r) tak, že úhel u B je tupý. Jak velký musí být úhel u vrcholu B čtyřúhelníku SCBA, aby byl tento úhel třikrát větší než vnitřní úhel ASC téhož čtyřúhelníku? - Vzdálenost středů
Na obrázku jsou kružnice k₁(S₁; r1=9 cm) a k₂(S2; r2 = 5 cm). Jejich průsečíky určují společnou tětivu t dlouhou 8 cm. Vypočítejte v cm vzdálenost středů |S₁ S₂| s přesností na dvě desetinná místa.
