Je dán 13
Je dán pravidelný čtyřboký hranol ABCDEFGH s podstavnou hranou AB délky 8 cm a výškou 6 cm. Bod M je střed hrany AE. Určete vzdálenost bodu M od roviny BDH.
Správná odpověď:
Tipy na související online kalkulačky
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
Související a podobné příklady:
- Vzdálenost bodů
Je dán pravidelný čtyřboký jehlan ABCDV, ve kterém AB = a = 4 cm a v = 8 cm. Nechť S je střed CV. Vypočítejte vzdálenost bodů A a S. - Průsečík přímky a roviny
Je dán pravidelný čtyřboký jehlan ABCDV, uvnitř jeho hrany AV je bod M, na prosloužené úsečce DC za bod C je bod N. Sestrojte průsečnici roviny MNV s rovinou BCV a průsečík přímky MN a roviny BCV. - Je dán 21
Je dán pravidelný čtyřboký jehlan s délkou podstavné hrany a=15cm a výškou v=21cm. Rovnoběžně s podstavou vedeme dvě roviny tak, že rozdělil výšku jehlanu na tři stejné části. Vypočítej poměr objemů vzniklých 3 těles. - Pravidelný 8 Pravidelný čtyřboký jehlan má podstavnou hranu a=1,56 dm a výšku v= 2,05dm. Vypočtěte : a) odchylku roviny boční stěny od roviny podstavy b) odchylku boční hrany od roviny podstavy
- Kvádr
Kvádr ABCDEFGH o výšce 10 cm má podstavné hrany délky 6 cm a 8 cm. Určete odchylku tělesové úhlopříčky od roviny podstavy (zaokrouhlete na stupně) - Máme pravidelný
Máme pravidelný čtyřboký jehlan s podstavnou hranou a=10 cm a výškou v=7cm. Vypočtěte 1/obsah podstavy 2/obsah pláště 3/povrch jehlanu 4/objem jehlanu - Čtyřboký jehlan
Odlitek tvaru pravidelného čtyřbokého jehlanu s podstavnou hranou délky 60 cm a výšce 5 cm je zhotoven z materiálu o hustotě 7,8 g/cm krychlové. Vypočítejte jeho hmotnost. - Vzdálenosti 64804
Dán je čtverec ABCD. Na jeho úhlopříčce AC leží bod E tak, že platí vzdálenost AB je rovna vzdálenosti AE. Jaká je velikost úhlu EBC? - Čtyřboký hranol 7
Pravidelný kolmý čtyřboký hranol s podstavnou hranou 10 cm má objem 10 dm³. Jaká je výška tohoto hranolu?
- Čtyřboký jehlan
Je dán pravidelný čtyřboký jehlan ABCDV; | AB | = 4cm; v = 6cm. Určete úhel přímek AD a BV. - Nad každou
Nad každou stěnou kostky s hranou a = 30 cm je sestrojen pravidelný čtyřboký jehlan s výškou 15 cm. Vypočtěte objem takto vzniklého tělesa. - Vzdálenost přímek
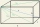Určite vzdálenost přímek AE, CG v kvádru ABCDEFGH, je-li dáno |AB| = 3cm, |AD| = 2 cm, |AE| = 4cm - Hrana
Je dán pravidelný čtyřboký jehlan, délka podstavne hrany je 6 cm a výška jehlanu je 10 cm. Vypočítej délku boční hrany. - Z7-1-6 MO 2018
Je dán rovnoramenný pravoúhlý trojúhelník ABS se základnou AB. Na kružnici, která má střed v bodě S a prochází body A a B, leží bod C tak, že trojúhelník ABC je rovnoramenný. Určete, kolik bodů C vyhovuje uvedeným podmínkám, a všechny takové body sestrojt
- Těžitko Vypočitej hmotnost těžítka tvaru pravidelného čtyřbokeho jehlanu s podstavnou hranou délky 5cm a tělesovou výškou 6,5cm , je li zhotoveno z materialu o hustotě 8 g/cm³.
- Čtyřboký jehlan 4
Je dán pravidelný čtyřboký jehlan s délkou podstavné hrany a = 3 cm a s délkou boční hrany h = 8 cm. Vypočítejte prosím jeho povrch a objem. - Čtyřboký jehlan 9
Je dán pravidelný čtyřboký jehlan. Délka hrany podstavy a = 6,5 cm, boční hrana s = 7,5 cm. Vypočítejte objem a obsah pláště.
