Absolutní hodnota - příklady
Pokyny: Každý problém vyřešte pečlivě a ukažte kompletní postup.Počet nalezených příkladů: 139
- Ve středu 2
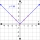 Ve středu mezi neznámým číslem a číslem 30 je číslo 12. Urči neznámé číslo.
Ve středu mezi neznámým číslem a číslem 30 je číslo 12. Urči neznámé číslo. - Vypočítej 449
 Vypočítej velikost úhlu, který svírají 2 úsečky na ciferníku a vzniknou spojením bodů 7, 2 a 1, 4.
Vypočítej velikost úhlu, který svírají 2 úsečky na ciferníku a vzniknou spojením bodů 7, 2 a 1, 4. - Převrácené číslo
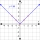 Co dostaneme vynásobením absolutní hodnoty k číslu -0,7 a převráceného čísla k číslu 10?
Co dostaneme vynásobením absolutní hodnoty k číslu -0,7 a převráceného čísla k číslu 10? - Souřadnice bodu
 Mám bod A=[2,1] a přímku y+x-5=0. Jak určím souřadnice bod A´, který je obrazem bodu A podle dané přímky?
Mám bod A=[2,1] a přímku y+x-5=0. Jak určím souřadnice bod A´, který je obrazem bodu A podle dané přímky? - Vzdálenost bodu od roviny
 Vypočítej vzdálenost bodu A[ 4; 2; -3 ] od roviny : 2x - 2y + z + 5 = 0
Vypočítej vzdálenost bodu A[ 4; 2; -3 ] od roviny : 2x - 2y + z + 5 = 0 - Vypočítejte kvádr
 Je dán kvádr ABCDEFGH. Víme, že |AB| = 1 cm, |BC| = 2 cm, |AE| = 3 cm. Vypočítejte ve stupních velikost úhlu, který svírají přímky BG a FH .
Je dán kvádr ABCDEFGH. Víme, že |AB| = 1 cm, |BC| = 2 cm, |AE| = 3 cm. Vypočítejte ve stupních velikost úhlu, který svírají přímky BG a FH . - Obkladači
 První obkladač by obložil vnitřek bazénu za 5 pracovních hodín, druhý by na stejnou práci potřeboval 7 pracovních hodín. Za kolik hodín by obložili vnitřek bazénu společně, jestliže druhý obkladač začne pracovat na bazénu o 12 minut později něž první?
První obkladač by obložil vnitřek bazénu za 5 pracovních hodín, druhý by na stejnou práci potřeboval 7 pracovních hodín. Za kolik hodín by obložili vnitřek bazénu společně, jestliže druhý obkladač začne pracovat na bazénu o 12 minut později něž první? - Rovnice paraboly
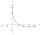 Určete rovnici paraboly, která má bod F = [3,2] za své ohniště a přímku x+y+1=0 za svou řadící přímku.
Určete rovnici paraboly, která má bod F = [3,2] za své ohniště a přímku x+y+1=0 za svou řadící přímku. - Rychlost koulí po srážce
 Dvě nepružné/plastické koule se pohybují proti sobě stejnými rychlostmi 2 m/s. Hmotnost jedné koule je 3kg, druhé 1kg. Určete rychlost koulí po srážce a úbytek kinetické energie.
Dvě nepružné/plastické koule se pohybují proti sobě stejnými rychlostmi 2 m/s. Hmotnost jedné koule je 3kg, druhé 1kg. Určete rychlost koulí po srážce a úbytek kinetické energie. - Digitální
 Digitální fotografie má rozměry 640 × 480 pixelů. Který z klasických papírových formátů fotografie je „nejpodobnější": 9 × 6 cm, 10 × 7 cm, 13 × 9 cm, 15 × 10 cm, 18 × 13 cm nebo 30 × 20 cm?
Digitální fotografie má rozměry 640 × 480 pixelů. Který z klasických papírových formátů fotografie je „nejpodobnější": 9 × 6 cm, 10 × 7 cm, 13 × 9 cm, 15 × 10 cm, 18 × 13 cm nebo 30 × 20 cm? - Jiho-západ
 Muž v poušti ujede 8,7 míle ve směru S 26° W (jiho-západ). Potom se otočí o 90° a přejde 9 mil ve směru na N 49° W (severo západně). Jak daleko je v té době od svého výchozího bodu a jeho postoj od jeho výchozího bodu?
Muž v poušti ujede 8,7 míle ve směru S 26° W (jiho-západ). Potom se otočí o 90° a přejde 9 mil ve směru na N 49° W (severo západně). Jak daleko je v té době od svého výchozího bodu a jeho postoj od jeho výchozího bodu? - Najděte číslo
 Najděte na číselné ose číslo, jehož vzdálenost od čísla 3 je čtyřikrát menší než od čísla 15 (určete obě řešení).
Najděte na číselné ose číslo, jehož vzdálenost od čísla 3 je čtyřikrát menší než od čísla 15 (určete obě řešení). - Vypočítej: 3
 Vypočítej: |7 − 15| + |8| − |−13| − 1 =
Vypočítej: |7 − 15| + |8| − |−13| − 1 = - Geometrické členy
 Najděte uvedený počet geometrických členů (průměrů) mezi dvojicí čísel. -32 a 4 [vložit 2 členy] Pořadí:-32, _, _, 4
Najděte uvedený počet geometrických členů (průměrů) mezi dvojicí čísel. -32 a 4 [vložit 2 členy] Pořadí:-32, _, _, 4 - Rychlost - letadlo
 Letadlo se pohybuje ve směru 45 stupňů severní šířky východu rychlostí 320 km/h, když narazí na proud z východu na jihu o rychlosti 115 stupňů 20 km/h. Jaký je nový kurz a rychlost letadla?
Letadlo se pohybuje ve směru 45 stupňů severní šířky východu rychlostí 320 km/h, když narazí na proud z východu na jihu o rychlosti 115 stupňů 20 km/h. Jaký je nový kurz a rychlost letadla? - Absolutní hodnoty
 Je možné pro |r| + |s| = |r+s|? Pokud ano, kdy?
Je možné pro |r| + |s| = |r+s|? Pokud ano, kdy? - Výběr vrtáku
 Billův 3/8 palcový vrták chybí a je potřebný k práci. Vystačí si s vyvrtáním menšího otvoru než 3/8 palce, pokud je co nejblíže 3/8 palců. Který z následujících bitů by bylo nejlépe použít? A. 13/32 palce B. 23/64 palce C. 1/2 palce D. 5/16 palce
Billův 3/8 palcový vrták chybí a je potřebný k práci. Vystačí si s vyvrtáním menšího otvoru než 3/8 palce, pokud je co nejblíže 3/8 palců. Který z následujících bitů by bylo nejlépe použít? A. 13/32 palce B. 23/64 palce C. 1/2 palce D. 5/16 palce - Diferenciální počet
 A). Načrtněte graf funkce f(x)=x * abs(x) = x * |x| b). Pro jaké hodnoty x je f(x) diferencovatelné c). Najít F(x)
A). Načrtněte graf funkce f(x)=x * abs(x) = x * |x| b). Pro jaké hodnoty x je f(x) diferencovatelné c). Najít F(x) - Obvod trojúhelníku
 Urči obvod trojúhelníku ABC kde bod A je začátek souřadnicové soustavy, bod B je průsečík grafu linearní funkce f: y = - 3/4• x + 3 s osou x a C je průsečík grafu této funkce s osou y.
Urči obvod trojúhelníku ABC kde bod A je začátek souřadnicové soustavy, bod B je průsečík grafu linearní funkce f: y = - 3/4• x + 3 s osou x a C je průsečík grafu této funkce s osou y. - Komplexní číslo
 Nechť komplexní číslo z=-√2-√2i, kde i² = -1. Najděte |z|, arg(z), z* (kde * označuje komplexní konjugát) a (1/z). V případě potřeby napište své odpovědi ve tvaru a + i b, kde ai b jsou reálná čísla. Označte polohy čísel z, z* a (1/z) na Argandově diagram
Nechť komplexní číslo z=-√2-√2i, kde i² = -1. Najděte |z|, arg(z), z* (kde * označuje komplexní konjugát) a (1/z). V případě potřeby napište své odpovědi ve tvaru a + i b, kde ai b jsou reálná čísla. Označte polohy čísel z, z* a (1/z) na Argandově diagram
Máš příklad z matematiky, který jsi tady nenašel vyřešený? Pošli nám příklad a my Ti ho zkusíme vypočítat.
