Podobnost trojúhelníků - příklady
Pokyny: Vyřešte každý úkol pečlivě a ukažte své celé řešení. Pokud je to vhodné, proveďte zkoušku správnosti řešení.Počet nalezených příkladů: 157
- Koeficient podobnosti
Dán je trojúhelník ABC se stranami a = 12 cm b = 9 cm c = 7 cm a trojúhelník DEF se stranami d = 8,4 cm, e = 6,3 cm f = 4,9 cm Zjisti zda jsou trojúhelníky ABC a DEF podobné pokud ano koeficient podobnosti a napiš podle které věty jsou podobné - Lichoběžník 83
Lichoběžník ABCD je složen z pěti trojúhelníků. Body E, G dělí úsečku AB v poměru 2:4:3 (v tomto pořadí) na tři úsečky. Bod F je středem úsečky AD. Trojúhelník AEF je rovnoramenný a pravoúhlý. Trojúhelníky GBC a CDG jsou pravoúhlé. Obsah trojúhelníku AEF - Rozhledna 3
Jak vysoká je rozhledna, jestliže vrhá stín dlouhý 9,6m přesně ve stejném okamžiku, kdy puůlmetrová tyč vrhá stín dlouhý 30 cm. - Trojúhelníky 83634
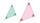Máme podobné trojúhelníky ABC s úhlem CAB=45° a úhlem ACB= 30° a podobný trojúhelník OPN. Jaký je úhel NOP na podobném trojúhelníku? - V trojúhelníku 10
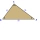V trojúhelníku ABC se velikost vnějšího úhlu při vrcholu C rovná 126°. Velikost vnitřních úhlů při vrcholech A, B jsou v poměru 5: 9. Vypočítej velikost vnitřních úhlů α, β, γ trojúhelníku ABC. - Trojúhelníku 83357
Vypočítejte poloměr kružnice opsaného trojúhelníku, který má rozměry stran 8, 10 a 14cm. - Z rozhledně
Z rozhledně vysoké 40 m je vidět vrchol topolu pod hloubkovym uhlem o velikosti 50°10' a patu topolu v hloubkovem úhlu o velikosti 58°. Vypocitejte výšku topolu.
- Vypočítejte 82693
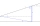Vypočítejte výšku stožáru, jehož patu vidíme v hloubkovém úhlu 11° a vrchol ve výškovém úhlu 28°. Stožár je pozorován z místa 10 m nad úrovní paty stožáru. - Školní 13 Školní budova vrhá na rovinu dvora stín 16 m dlouhý a v téže době vrhá svislá metrová tyč stín 132 cm dlouhý. Určete výšku budovy.
- Přesýpací hodiny
Přesýpací hodiny sestávají ze dvou shodných nádobek ve tvaru rotačních kuželů. Pro jednoduchost předpokládáme, že koužely se dotýkají pouze svými vrcholy. Písek sahá do poloviny výšky spodního kužele. Po překlopení hodí trvá přesně 21 minut, než se písek - Výběr 4
Výběr trojúhelník, který je podobný zadanému trojúhelníku RTG. ∆ RTG, r= 24 dm, t = 28 dm, g= 30 dm. ∆ SHV= 6 dm, h= 7,5 dm, v= 7 dm ∆ VSH= v= 7 dm, s= 6 dm, h= 7,5 dm ∆ HVS= h= 7,5 dm, v= 7 dm, s = 6 dm. ∆ VHS= v= 7 dm, h = 7,5 dm, s= 6 dm. ∆ HSV= h= 7,5 - Vyber 3
Vyber trojúhelník, který je podobný zadanému trojúhelníku. - ∆ TFC= t= 8 cm, f= 9 cm, c= 7 cm. : ∆ PKU= p= 45 cm, k= 35 cm, u= 40 cm. ∆ UPK= u= 40 cm, p= 45 cm, k= 35 cm. ∆ PUK= p= 45 cm, u= 40 cm, k= 35 cm. ∆ KPU= k= 35 cm, p= 45 cm, u= 40 cm. ∆ KUP= k= - Rozhodni 3 Rozhodni, jestli jsou trojúhelníky podobné. Vyber mezi Ano/Ne. ∆ YUO: y= 9m, u= 17 m, o= 12 m, ∆ ZXV= z= 207 dm, x= 341 dm, v= 394 dm
- Trojúhelníku 80859
Trojúhelník ABC a trojúhelník ADE jsou podobné. Vypočítejte v centimetrech čtverečních obsah trojúhelníku ABC, pokud délka strany DE je 12 cm, délka strany BC je 16 cm a obsah trojúhelníku ADE je 27 cm². - Trojúhelníkem 80754 Obvod trojúhelníku MAK je 216 mm, strana a = 81 mm a strana k = 62 mm. Urč délku strany z trojúhelníku OSA, pokud platí, že trojúhelník MAK je shodný s trojúhelníkem OSA.
- Trojúhelníku 80745 Obsah pravoúhlého trojúhelníku KLM s pravým úhlem u vrcholu L je 60 mm čtverečních a jeho odvěsna k má délku 10 mm. Trojúhelníky KLM a RST jsou podobné, poměr podobnosti je k=2,5 . Vypočítej obsah trojúhelníku RST.
- Trojúhelníku 80742
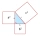Vypočítej obvod trojúhelníku ABC, pokud víš, že je podobný trojúhelníku EFG, ve kterém e=144 mm, f=164 mm, g=92 mm a poměr podobnosti je 4. Výsledek vyjádři v cm. - Vypočítej 80741
V táboře dělaly děti maketu tábořiště. V jejím středu byl javor který na maketě měl výšku 28 cm. Vypočítej jakou výšku má javor v tábořišti pokud ráno vrhá stín 14 m dlouhý a jeho maketa má tehdy stín 49 cm dlouhý. - Náhrdelník 77664
Nicolette vyrábí malý korálkový náramek z 5 červených korálků, 8 fialových korálků a 6 zelených korálků. Velký náhrdelník má stejný poměr korálků jako malý náramek. Pokud velký náhrdelník vyžaduje 15 červených kuliček, kolik fialových kuliček je zapotřebí - Aritmetickou 76704
Najděte všechny pravoúhlé trojúhelníky, jejichž délky stran tvoří aritmetickou posloupnost.
Máš příklad, nad kterým si přemýšlíš alespoň 10 minut? Pošli nám příklad a my Ti ho zkusíme vypočítat.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
